题目内容
【题目】如图,y关于x的二次函数y=﹣![]() (x+m)(x﹣3m)图象的顶点为M,图象交x轴于A、B两点,交y轴正半轴于D点.以AB为直径作圆,圆心为C.定点E的坐标为(﹣3,0),连接ED.(m>0)
(x+m)(x﹣3m)图象的顶点为M,图象交x轴于A、B两点,交y轴正半轴于D点.以AB为直径作圆,圆心为C.定点E的坐标为(﹣3,0),连接ED.(m>0)
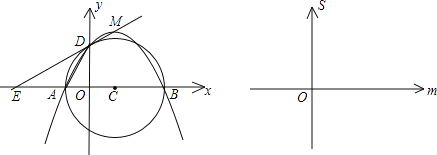
(1)写出A、B、D三点的坐标;
(2)当m为何值时M点在直线ED上?判定此时直线与圆的位置关系;
(3)当m变化时,用m表示△AED的面积S,并在给出的直角坐标系中画出S关于m的函数图象的示意图.
【答案】(1)A(﹣m,0),B(3m,0),D(0,![]() m).(2)直线ED与⊙C相切.(3)见解析
m).(2)直线ED与⊙C相切.(3)见解析
【解析】
试题分析:(1)根据x轴,y轴上点的坐标特征代入即可求出A、B、D三点的坐标;
(2)待定系数法先求出直线ED的解析式,再根据切线的判定得出直线与圆的位置关系;
(3)分当0<m<3时,当m>3时两种情况讨论求得关于m的函数.
解:(1)令y=0,则﹣![]() (x+m)(x﹣3m)=0,解得x1=﹣m,x2=3m;
(x+m)(x﹣3m)=0,解得x1=﹣m,x2=3m;
令x=0,则y=﹣![]() (0+m)(0﹣3m)=
(0+m)(0﹣3m)=![]() m.
m.
故A(﹣m,0),B(3m,0),D(0,![]() m).
m).
(2)设直线ED的解析式为y=kx+b,将E(﹣3,0),D(0,![]() m)代入得:
m)代入得:
![]()
解得,k=![]() ,b=
,b=![]() m.
m.
∴直线ED的解析式为y=![]() mx+
mx+![]() m.
m.
将y=﹣![]() (x+m)(x﹣3m)化为顶点式:y=﹣
(x+m)(x﹣3m)化为顶点式:y=﹣![]() (x﹣m)2+
(x﹣m)2+![]() m.
m.
∴顶点M的坐标为(m,![]() m).代入y=
m).代入y=![]() mx+
mx+![]() m得:m2=m
m得:m2=m
∵m>0,
∴m=1.所以,当m=1时,M点在直线DE上.
连接CD,C为AB中点,C点坐标为C(m,0).
∵OD=![]() ,OC=1,
,OC=1,
∴CD=2,D点在圆上
又∵OE=3,DE2=OD2+OE2=12,
EC2=16,CD2=4,
∴CD2+DE2=EC2.
∴∠EDC=90°
∴直线ED与⊙C相切.
(3)当0<m<3时,S△AED=![]() AE.OD=
AE.OD=![]() m(3﹣m)
m(3﹣m)
S=﹣![]() m2+
m2+![]() m.
m.
当m>3时,S△AED=![]() AEOD=
AEOD=![]() m(m﹣3).
m(m﹣3).
即S=![]() m2_
m2_ ![]() m.
m.
S关于m的函数图象的示意图如右: