��Ŀ����
����Ŀ����ͼ���ڷ���ֽ�У�������ABC����������͵�P����С����Ķ����ϣ�

��1������ͼ1�У�������������ABC�Ƶ�C��ת���������A1B1C��ʹ�õ�P����������A1B1C�ڲ�����������A1B1C�Ķ���Ҳ�����ڷ���Ķ����ϣ�
��2��д����ת�ǵĶ��� ��
��3����չ���죺��ͼ2����ֱ��������ABC��������C=90�����Ƶ�A��˳ʱ�뷽��ѡ��115���õ���AB1C1��ʹ�õ�C��A��B1��ͬһ��ֱ���ϣ���ô��BAC1���� ��
���𰸡���1������������2��90������3��50����
��������
�����������1������ͼ����ת�����ʣ�����ȷ��A��B�Ķ�Ӧ��A1��B1�������Ӽ��ɻ�����A1B1C���ɣ�
��2��������ת��ͼ�ε�λ��д����ת�Ƕȣ�
��3�����ȼ������BAC���ٸ�����ת�ɵ���BAC=��C1AB1=65�����ٸ��ݽǵĺͲ��ϵ�ɵô𰸣�
�⣺��1����ͼ��ʾ��
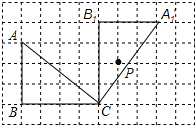
��2����ת�ǵĶ���Ϊ90����
��3������C��A��B1��ͬһ��ֱ���ϣ�
���CAB1=180����
���Ƶ�A��˳ʱ�뷽��ѡ��115����
���BAC=180����115��=65����
������ת�ɵ���BAC=��C1AB1=65����
���BAC1=180�㩁65�㩁65��=50����
�ʴ�Ϊ��50����

 ϰ�⾫ѡϵ�д�
ϰ�⾫ѡϵ�д�