题目内容
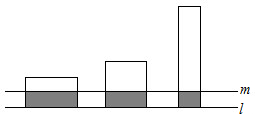 如图,在直线l上平放有3个面积相等的矩形,其高分别为2m,3m,6m,现作一平行于l的直线m,使截得三部分阴影面积之和恰好等于一个矩形的面积,则l,m之间的距离应为
如图,在直线l上平放有3个面积相等的矩形,其高分别为2m,3m,6m,现作一平行于l的直线m,使截得三部分阴影面积之和恰好等于一个矩形的面积,则l,m之间的距离应为1m
1m
.分析:设三个矩形的长是am、bm、cm,得出2a=3b=6c,求出b=
a,c=
a,设l、m之间的距离是xm,得出方程ax+bx+cx=2a,把b、c的值代入求出方程的解即可.
| 2 |
| 3 |
| 1 |
| 3 |
解答:解:设三个矩形的长是am、bm、cm,
则2a=3b=6c,
解得:b=
a,c=
a,
设l、m之间的距离是xm,
则ax+bx+cx=2a,
即ax+
ax+
ax=2a,
解得:x=1.
故答案为:1m.
则2a=3b=6c,
解得:b=
| 2 |
| 3 |
| 1 |
| 3 |
设l、m之间的距离是xm,
则ax+bx+cx=2a,
即ax+
| 2 |
| 3 |
| 1 |
| 3 |
解得:x=1.
故答案为:1m.
点评:本题考查了矩形的性质的应用,关键是把实际问题转化成数学问题,主要考查了学生的分析问题和解决问题的能力,题型较好,有一定的难度.

练习册系列答案
相关题目
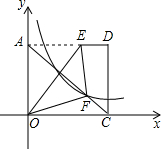 如图,将矩形AOCD平放在平面直角坐标系中,E是边AD上的点,若沿着OE所在直线对折,点A恰好落在对角线AC上的F点处,已知AE=4,OC=5,双曲线y=
如图,将矩形AOCD平放在平面直角坐标系中,E是边AD上的点,若沿着OE所在直线对折,点A恰好落在对角线AC上的F点处,已知AE=4,OC=5,双曲线y=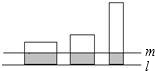 如图,在直线l上平放有3个面积相等的矩形,其高分别为2m,3m,6m.现作一平行于l的直线m,使截得三部分阴影面积之和恰好等于一个矩形面积,求l,m之间的距离.
如图,在直线l上平放有3个面积相等的矩形,其高分别为2m,3m,6m.现作一平行于l的直线m,使截得三部分阴影面积之和恰好等于一个矩形面积,求l,m之间的距离. 如图,在直线l上平放有3个面积相等的矩形,其高分别为2m,3m,6m,现作一平行于l的直线m,使截得三部分阴影面积之和恰好等于一个矩形的面积,则l,m之间的距离应为________.
如图,在直线l上平放有3个面积相等的矩形,其高分别为2m,3m,6m,现作一平行于l的直线m,使截得三部分阴影面积之和恰好等于一个矩形的面积,则l,m之间的距离应为________.