题目内容
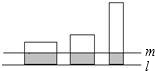 如图,在直线l上平放有3个面积相等的矩形,其高分别为2m,3m,6m.现作一平行于l的直线m,使截得三部分阴影面积之和恰好等于一个矩形面积,求l,m之间的距离.
如图,在直线l上平放有3个面积相等的矩形,其高分别为2m,3m,6m.现作一平行于l的直线m,使截得三部分阴影面积之和恰好等于一个矩形面积,求l,m之间的距离.分析:要求出l,m之间的距离,就要先设出未知数,再通过理解题意找出本题的等量关系,在列出方程求解.
解答:解:设三个矩形底边长分别为a,b,c,矩形面积为S,l,m之间的距离为x,
则有2a=3b=6c=S,且(a+b+c)x=S,
即:a=
,b=
,c=
;代入(a+b+c)x=S后
可解得x=1(m).
答:l,m之间的距离为1m.
故答案为1m.
则有2a=3b=6c=S,且(a+b+c)x=S,
即:a=
| S |
| 2 |
| S |
| 3 |
| S |
| 6 |
可解得x=1(m).
答:l,m之间的距离为1m.
故答案为1m.
点评:解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
相关题目
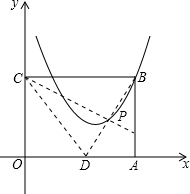
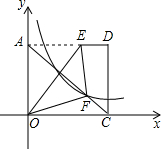 如图,将矩形AOCD平放在平面直角坐标系中,E是边AD上的点,若沿着OE所在直线对折,点A恰好落在对角线AC上的F点处,已知AE=4,OC=5,双曲线y=
如图,将矩形AOCD平放在平面直角坐标系中,E是边AD上的点,若沿着OE所在直线对折,点A恰好落在对角线AC上的F点处,已知AE=4,OC=5,双曲线y=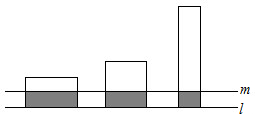 如图,在直线l上平放有3个面积相等的矩形,其高分别为2m,3m,6m,现作一平行于l的直线m,使截得三部分阴影面积之和恰好等于一个矩形的面积,则l,m之间的距离应为
如图,在直线l上平放有3个面积相等的矩形,其高分别为2m,3m,6m,现作一平行于l的直线m,使截得三部分阴影面积之和恰好等于一个矩形的面积,则l,m之间的距离应为 如图,在直线l上平放有3个面积相等的矩形,其高分别为2m,3m,6m,现作一平行于l的直线m,使截得三部分阴影面积之和恰好等于一个矩形的面积,则l,m之间的距离应为________.
如图,在直线l上平放有3个面积相等的矩形,其高分别为2m,3m,6m,现作一平行于l的直线m,使截得三部分阴影面积之和恰好等于一个矩形的面积,则l,m之间的距离应为________.