题目内容
【题目】如图,∠MON=90°,点A,B分别在射线OM,ON上移动,∠OAB的平分线与∠OBA的外角平分线交于点C,试猜想:随着点A,B的移动,∠ACB的大小是否发生变化,并说明理由.
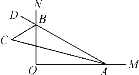
【答案】∠ACB的大小不发生变化
【解析】
根据三角形的一个外角等于和它不相邻的两个内角的和,∠OBD=∠OAB+∠MON,∠CBD=∠ACB+∠CAB,再根据角平分线的定义∠BAC=![]() ∠OAB,∠CBD=
∠OAB,∠CBD=![]() ∠OBD,代入整理即可得到∠ACB=
∠OBD,代入整理即可得到∠ACB=![]() ∠MON=45°.
∠MON=45°.
∠ACB的大小不变.
理由:∵AC平分∠OAB(已知),
∴∠BAC=![]() ∠OAB(角平分线的定义),
∠OAB(角平分线的定义),
∵BC平分∠OBD(已知),
∴∠CBD=![]() ∠OBD(角平分线定义),
∠OBD(角平分线定义),
∠OBD=∠MON+∠OAB(三角形的外角性质),∠CBD=∠ACB+∠BAC(三角形的外角性质),
∴∠ACB=∠CBD-∠BAC=![]() (∠MON+∠OAB)-
(∠MON+∠OAB)-![]() ∠OAB=
∠OAB=![]() ∠MON=
∠MON=![]() ×90°=45°.
×90°=45°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目