题目内容
【题目】某商店试销一种新商品,该商品的进价为40元/件,经过一段时间的试销发现,每月的销售量会因售价在40~70元之间的调整而不同.当售价在40~50元时,每月销售量都为60件;当售价在50~70元时,每月销售量与售价的关系如图所示,令每月销售量为y件,售价为x元/件,每月的总利润为Q元. 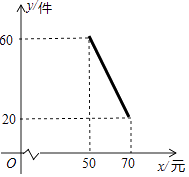
(1)当售价在50~70元时,求每月销售量为y与x的函数关系式?
(2)当该商品售价x是多少元时,该商店每月获利最大,最大利润是多少元?
(3)若该商店每月采购这种新商品的进货款不低于1760元,则该商品每月最大利润为元.
【答案】
(1)解:令y=kx+b
由图知:当x=50时,y=60;当x=70时,y=20.
∴ ![]() ,
,
∴ ![]() ,
,
∴y=﹣2x+160(50≤x≤70);
(2)解:由题可知,
当40≤x≤50时,Q=60(x﹣40)=60x﹣2400,
∵60>0,
∴Q随x的增大而增大,
∴x=50时,Q有最大值600元.
当50≤x≤70时,Q=y(x﹣40)=2x2+240x﹣6400=﹣2(x﹣60)2+800,
∵﹣2<0,
∴x=60时,Q有最大值800元.
综上所述,当该商品售价是60元时,该商店每月获利最大,最大利润是800元.
(3)792
【解析】解:(3)设采购的数量为m,则40m≥1760,解得m≥44, 由(1)知,若40≤x≤50,则利润的最大值为600元;
若50≤x≤70,由﹣2x+160≥44可得x≤58,
∵Q=﹣2(x﹣60)2+800中x<60时,Q随x的增大而增大,
∴当x=58时,Q取得最大值,最大值为792,
故答案为:792.
(1)待定系数法求解可得;(2)分40≤x≤50和50≤x≤70两种情况,根据总利润=单件利润×销售量列出函数解析式,根据函数性质解答可得;(3)由进货款求得进货量的范围,结合(2)中的函数解析式分类讨论求解可得.

【题目】光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台,先将这50台联合收割机派往A、B两地区收割小麦,其中30台派往A地区,20台派往B地区.两地区与该农机租赁公司商定的每天的租赁价格见表:
每台甲型收割机的租金 | 每台乙型收割机的租金 | |
A地区 | 1800 | 1600 |
B地区 | 1600 | 1200 |
(1)设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),求y与x间的函数关系式,并写出x的取值范围;
(2)若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79 600元,说明有多少种分配方案,并将各种方案设计出来;
(3)如果要使这50台联合收割机每天获得的租金最高,请你为光华农机租赁公司提一条合理化建议.