题目内容
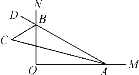
【题目】如图,在平面直角坐标系xOy中,直线y=﹣2x+a与y轴交于点C (0,6),与x轴交于点B.

(1)求这条直线的解析式;
(2)直线AD与(1)中所求的直线相交于点D(﹣1,n),点A的坐标为(﹣3,0).
①求n的值及直线AD的解析式;
②求△ABD的面积;
③点M是直线y=﹣2x+a上的一点(不与点B重合),且点M的横坐标为m,求△ABM的面积S与m之间的关系式.
【答案】(1)y=﹣2x+6(2)①y=4x+12 ②24 ③S=6m-18.
【解析】试题分析:(1)利用待定系数法可求函数的解析式;
(2)①根据题意直接代入函数的解析式求出n,得到D点的坐标,然后由A、D点的坐标,由待定系数法求出AD的解析式;
②构造三角形直接求面积;
③由点M在直线y=-2x+6得到M的坐标,构造三角形,然后分类求解即可.
试题解析:(1)∵直线y=﹣2x+a与y轴交于点C (0,6),∴a=6,
∴该直线解析式为y=﹣2x+6.

(2)①∵点D(﹣1,n)在直线BC上,
∴n=﹣2×(﹣1)+6=8,
∴点D(﹣1,8).
设直线AD的解析式为y=kx+b,
将点A(﹣3,0)、D(﹣1,8)代入y=kx+b中,
得:![]() ,解得:
,解得:![]() ,
,
∴直线AD的解析式为y=4x+12.
②令y=﹣2x+6中y=0,则﹣2x+6=0,解得:x=3,∴点B(3,0).
∵A(﹣3,0)、D(﹣1,8),∴AB=6.
S△ABD=![]() AByD=
AByD=![]() ×6×8=24
×6×8=24
③∵点M在直线y=-2x+6上,∴M(m,-2m+6),
![]()
当m<3时,S=![]()
即![]() ;
;
当m>3时, ![]()
即S=6m-18.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目