Question

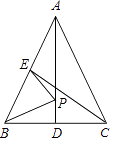
【题目】如图，将边长为6的正三角形纸片ABC按如下顺序进行两次折叠，展平后，得折痕AD，BE（如图①），点O为其交点．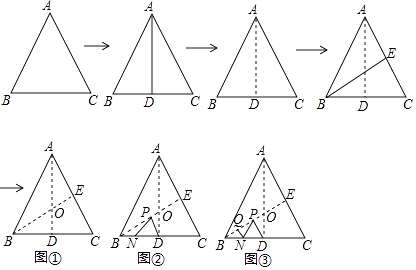

（1）探求AO到OD的数量关系，并说明理由；
（2）如图②，若P，N分别为BE，BC上的动点．
（Ⅰ）当PN+PD的长度取得最小值时，求BP的长度；
（Ⅱ）如图③，若点Q在线段BO上，BQ=1，则QN+NP+PD的最小值= ．

Answer 1

【答案】
（1）

解：AO=2OD，

理由：∵△ABC是等边三角形，

∴∠BAO=∠ABO=∠OBD=30°，

∴AO=OB，

∵BD=CD，

∴AD⊥BC，

∴∠BDO=90°，

∴OB=2OD，

∴OA=2OD；

（2）

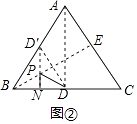
如图②，作点D关于BE的对称点D′，过D′作D′N⊥BC于N交BE于P，

则此时PN+PD的长度取得最小值，

∵BE垂直平分DD′，

∴BD=BD′，

∵∠ABC=60°，

∴△BDD′是等边三角形，

∴BN= BD= ，

∵∠PBN=30°，

∴ = ，

∴PB= ；

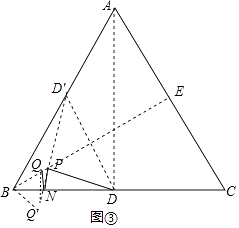
如图③，作Q关于BC的对称点Q′，作D关于BE的对称点D′，

连接Q′D′，即为QN+NP+PD的最小值．

根据轴对称的定义可知：∠Q′BN=∠QBN=30°，∠QBQ′=60°，

∴△BQQ′为等边三角形，△BDD′为等边三角形，

∴∠D′BQ′=90°，

∴在Rt△D′BQ′中，

D′Q′= = ．

∴QN+NP+PD的最小值= ，

故答案为： ．

【解析】（1）根据等边三角形的性质得到∠BAO=∠ABO=∠OBD=30°，得到AO=OB，根据直角三角形的性质即可得到结论；（2）（Ⅰ）如图②，作点D关于BE的对称点D′，过D′作D′N⊥BC于N交BE于P，则此时PN+PD的长度取得最小值，根据线段垂直平分线的想知道的BD=BD′，推出△BDD′是等边三角形，得到BN= BD= ，于是得到结论；（Ⅱ）如图③，作Q关于BC的对称点Q′，作D关于BE的对称点D′，连接Q′D′，即为QN+NP+PD的最小值．根据轴对称的定义得到∠Q′BN=∠QBN=30°，∠QBQ′=60°，得到△BQQ′为等边三角形，△BDD′为等边三角形，解直角三角形即可得到结论．
【考点精析】关于本题考查的三角形的“三线”，需要了解1、三角形角平分线的三条角平分线交于一点(交点在三角形内部，是三角形内切圆的圆心，称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部，是三角形的几何中心，称为中心);3、三角形的高线是顶点到对边的距离；注意：三角形的中线和角平分线都在三角形内才能得出正确答案．