题目内容
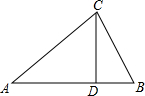
如图，在△ABC中，CD⊥AB于D，AC=4，BC=3，DB=
．
（1）求CD，AD的值；
（2）判断△ABC的形状，并说明理由．
| 9 |
| 5 |
（1）求CD，AD的值；
（2）判断△ABC的形状，并说明理由．
（1）∵CD⊥AB且CB=3，BD=
，故△CDB为直角三角形，
∴在Rt△CDB中，CD=
=
=
，
在Rt△CAD中，AD=
=
=
．
（2）△ABC为直角三角形．
理由：∵AD=
，BD=
，∴AB=AD+BD=
+
=5，
∴AC2+BC2=42+32=25=52=AB2，
∴根据勾股定理的逆定理，△ABC为直角三角形．
| 9 |
| 5 |
∴在Rt△CDB中，CD=
| CB2-BD2 |
32-(
|
| 12 |
| 5 |
在Rt△CAD中，AD=
| AC2-CD2 |
42-(
|
| 16 |
| 5 |
（2）△ABC为直角三角形．
理由：∵AD=
| 16 |
| 5 |
| 9 |
| 5 |
| 16 |
| 5 |
| 9 |
| 5 |
∴AC2+BC2=42+32=25=52=AB2，
∴根据勾股定理的逆定理，△ABC为直角三角形．
练习册系列答案
开心蛙口算题卡系列答案
相关题目
