题目内容
已知半径为2的⊙O中，弦AB=2
，则弦AB所对圆周角的度数______．
| 3 |
如图所示，
连接OA、OB，过O作OF⊥AB，则AF=AB，∠AOF=∠AOB，
∵OA=3，AB=2
，
∴AF=
AB=
×2
=
，
∴sin∠AOF=
=
，
∴∠AOF=60°，
∴∠AOB=2∠AOF=120°，
∴∠ADB=
∠AOB=
×120°=60°，
∴∠AEB=180°-60°=120°．
故答案为：60°或120°．
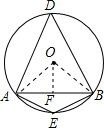
连接OA、OB，过O作OF⊥AB，则AF=AB，∠AOF=∠AOB，
∵OA=3，AB=2
| 3 |
∴AF=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴sin∠AOF=
| AF |
| OA |
| ||
| 2 |
∴∠AOF=60°，
∴∠AOB=2∠AOF=120°，
∴∠ADB=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠AEB=180°-60°=120°．
故答案为：60°或120°．
练习册系列答案
相关题目
段AC上，设AP=x（cm），OP=y（cm）．
