题目内容
【题目】如图,在ABCD中,延长AB到点E,使BE=AB,连接DE交BC于点F,则下列结论不一定成立的是( ) 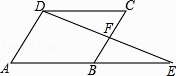
A.∠E=∠CDF
B.EF=DF
C.AD=2BF
D.BE=2CF
【答案】D
【解析】解:∵四边形ABCD是平行四边形, ∴CD//AB,
∴∠E=∠CDF,(故A成立);
∵四边形ABCD是平行四边形,
∴CD=AB,CD//BE,
∴∠C=∠CBE,
∵BE=AB,
∴CD=EB,
在△CDF和△BEF中,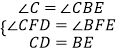 ,
,
∴△DCF≌△EBF(AAS),
∴EF=DF,(故B成立);
∵△DCF≌△EBF,
∴CF=BF= ![]() BC,
BC,
∵AD=BC,
∴AD=2BF,(故C成立);
∵AD≠BE,
∴2CF≠BE,(故D不成立);
故选:D.
首先根据平行四边形的性质可得CD//AB,再根据平行线的性质可得∠E=∠CDF;首先证明△DCF≌△EBF可得EF=DF;根据全等可得CF=BF= ![]() BC,再利用等量代换可得AD=2BF;根据题意不能证明AD=BE,因此BE不一定等于2CF.
BC,再利用等量代换可得AD=2BF;根据题意不能证明AD=BE,因此BE不一定等于2CF.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目