题目内容
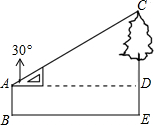
如图,一艘货轮向正北方向航行,在点A处测得灯塔M在北偏西30°,货轮以每小时20海里的速度航行,1小时后到达B处,测得灯塔M在北偏西45°,问该货轮到达灯塔正东方向D处时,货轮与灯塔M的距离是多少?
(精确到0.1海里,
≈1.732)

(精确到0.1海里,
| 3 |

由题意,得AB=20×1=20(海里).
直角三角形MDB中,BD=MD•cot45°=MD,
直角三角形AMD中,AD=MD•cot30°=
MD.
∵AB=AD-BD=(
-1)MD=20,
∴MD=10(
+1)≈27.3(海里).
答:货轮到达灯塔正东方向的D处时,货轮与灯塔的距离约为27.3海里.
直角三角形MDB中,BD=MD•cot45°=MD,
直角三角形AMD中,AD=MD•cot30°=
| 3 |
∵AB=AD-BD=(
| 3 |
∴MD=10(
| 3 |
答:货轮到达灯塔正东方向的D处时,货轮与灯塔的距离约为27.3海里.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
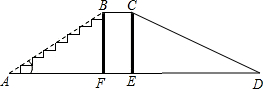 F均在线段AD上,四边形BCEF是矩形,且sin∠BAF=
F均在线段AD上,四边形BCEF是矩形,且sin∠BAF=

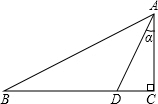
 同一条直线上.求电视塔OC的高度以及此人所在位置点P的铅直高度.(测倾器的高度忽略不计,结果保留根号形式)
同一条直线上.求电视塔OC的高度以及此人所在位置点P的铅直高度.(测倾器的高度忽略不计,结果保留根号形式)