题目内容
【题目】定义:和三角形一边和另两边的延长线同时相切的圆叫做三角形这边上的旁切圆.
如图所示,已知:⊙I是△ABC的BC边上的旁切圆,E、F分别是切点,AD⊥IC于点D.
(1)试探究:D、E、F三点是否同在一条直线上?证明你的结论.
(2)设AB=AC=5,BC=6,如果△DIE和△AEF的面积之比等于m,![]() ,试作出分别以
,试作出分别以![]() ,
,![]() 为两根且二次项系数为6的一个一元二次方程.
为两根且二次项系数为6的一个一元二次方程.

【答案】(1) D、E、F三点是同在一条直线上.(2) 6x2﹣13x+6=0.
【解析】
(1)利用切线长定理及梅氏定理即可求证;
(2)利用相似和韦达定理即可求解.
解:(1)结论:D、E、F三点是同在一条直线上.
证明:分别延长AD、BC交于点K,
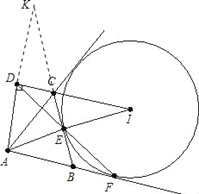
由旁切圆的定义及题中已知条件得:AD=DK,AC=CK,
再由切线长定理得:AC+CE=AF,BE=BF,
∴KE=AF.∴![]() ,
,
由梅涅劳斯定理的逆定理可证,D、E、F三点共线,
即D、E、F三点共线.
(2)∵AB=AC=5,BC=6,
∴A、E、I三点共线,CE=BE=3,AE=4,
连接IF,则△ABE∽△AIF,△ADI∽△CEI,A、F、I、D四点共圆.
设⊙I的半径为r,则:![]() ,
,
∴![]() ,即
,即![]() ,
,![]() ,
,
∴由△AEF∽△DEI得:
![]() ,
,
∴![]() .
.
∴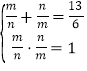 ,
,
因此,由韦达定理可知:分别以![]() 、
、![]() 为两根且二次项系数为6的一个一元二次方程是6x2﹣13x+6=0.
为两根且二次项系数为6的一个一元二次方程是6x2﹣13x+6=0.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目