题目内容
【题目】已知![]() 中,
中,![]() ,
,![]() ,过顶点
,过顶点![]() 作射线
作射线![]() .
.
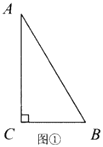
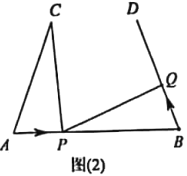
(1)当射线![]() 在
在![]() 外部时,如图①,点
外部时,如图①,点![]() 在射线
在射线![]() 上,连结
上,连结![]() 、
、![]() ,已知
,已知![]() ,
,![]() ,
,![]() (
(![]() ).
).
①试证明![]() 是直角三角形;
是直角三角形;
②求线段![]() 的长.(用含
的长.(用含![]() 的代数式表示)
的代数式表示)
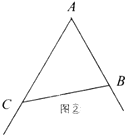
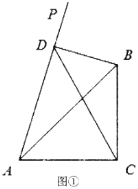
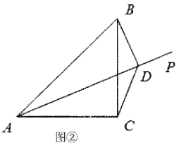
(2)当射线![]() 在
在![]() 内部时,如图②,过点
内部时,如图②,过点![]() 作
作![]() 于点
于点![]() ,连结
,连结![]() ,请写出线段
,请写出线段![]() 、
、![]() 、
、![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
【答案】(1)①详见解析;(2)![]() (
(![]() );(2)
);(2)![]() ,理由详见解析.
,理由详见解析.
【解析】
(1)①根据勾股定理的逆定理进行判断;
②过点C作CE⊥CD交DB的延长线于点E,利用同角的余角相等证明∠3=∠4,∠1=∠E,进而证明△ACD≌△BCE,求出DE的长,再利用勾股定理求解即可.
(2)过点C作CF⊥CD交BD的延长线于点F,先证∠ACD=∠BCF,再证△ACD≌△BCF,得CD=CF,AD=BF,再利用勾股定理求解即可.
(1)①∵![]()
![]()
又∵![]()
∴![]()
∴△ABD是直角三角形
②如图①,过点C作CE⊥CD交DB的延长线于点E,
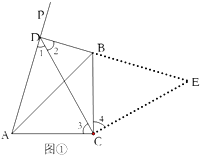
∵∠3+∠BCD=∠ACD=90°,∠4+∠BCD=∠DCE=90°
∴∠3=∠4
由①知△ABD是直角三角形
∴![]()
又∵![]()
∴∠1=∠E
在![]() 和
和![]() 中,
中,
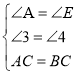
∴△ACD≌△BCE
∴![]() ,
,![]()
∴![]()
又∵![]() ,
,![]()
∴由勾股定理得![]()
∴![]()
![]() (
(![]() )
)
(2)AD、BD、CD的数量关系为:![]() ,
,
理由如下:
如图②,过点C作CF⊥CD交BD的延长线于点F,
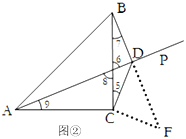
∵∠ACD=90°+∠5,∠BCF=90°+∠5
∴∠ACD=∠BCF
∵BD⊥AD
∴∠ADB=90°
∴∠6+∠7=90°
∵∠ACB=90°
∴∠9=∠8=90°
又∵∠6=∠8
∴∠7=∠9
![]() 和
和![]() 中
中
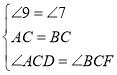
∴△ACD≌△BCF
∴CD=CF,AD=BF
又∵∠DCF=90°
∴由勾股定理得![]()
又DF=BF-BD=AD-BD
∴![]()

练习册系列答案
相关题目