题目内容
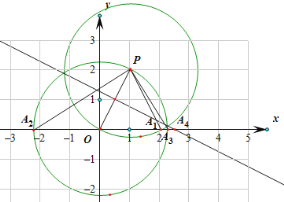
【题目】直角坐标系中已知点P（1，2），在x轴上找一点A，使△AOP为等腰三角形，这样的点A共有____个．
【答案】4
【解析】
要使△AOP为等腰三角形，只需分两种情况考虑：OP当底边或OP当腰，当OP是底边时，则点A即为OP的垂直平分线和x轴的交点；当OP是腰时，则点A即为分别以O、P为圆心，以OP为半径的圆和x轴的交点（点O除外），从而得出答案．
解：（1）若AO作为腰时，有两种情况，当P是顶角顶点时，A是以P为圆心，以OP为半径的圆与x轴的交点，共有1个，
当O是顶角顶点时，A是以O为圆心，以OP为半径的圆与x轴的交点，有2个；
（2）若OP是底边时，A是OP的中垂线与x轴的交点，有1个．
以上4个交点没有重合的．
故符合条件的点有4个．
故答案为：4．
练习册系列答案
小夫子全能检测系列答案
相关题目
【题目】2018年8月1日，郑州市物价局召开居民使用天然气销售价格新闻通气会，宣布郑州市天然气价格调整方案如下：
一户居民一个月天然气用量的范围 | 天然气价格（单位：元/立方米） |
不超过50立方米 | 2.56 |
超过50立方米的部分 | 3.33 |
（1）若张老师家9月份使用天然气36立方米，则需缴纳天然气费为______元；
（2）若张老师家10月份使用天然气
立方米，则需缴纳的天然气费为_______元；
（3）依此方案计算，若张老师家11月份实际缴纳天然气费201.26元，求张老师家11月份使用天然气多少立方米？
