Question

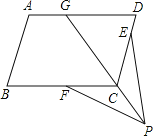
【题目】如图，点G、E、F分别在平行四边形ABCD的边AD、DC和BC上，DG=DC，CE=CF，点P是射线GC上一点，连接FP，EP．

求证：FP=EP．

Answer 1

【答案】证明见解析

【解析】证明：∵四边形ABCD是平行四边形，∴AD∥BC。∴∠DGC=∠GCB，

∵DG=DC，∴∠DGC=∠DCG。∴∠DCG=∠GCB。

∵∠DCG+∠DCP=180°，∠GCB+∠FCP=180°，∴∠DCP=∠FCP。

∵在△PCF和△PCE中，CE=CF，∠FCP=∠ECP，CP=CP，

∴△PCF≌△PCE（SAS）。∴PF=PE。

根据平行四边形的性质推出∠DGC=∠GCB，根据等腰三角形性质求出∠DGC=∠DCG，推出∠DCG=∠GCB，根据等角的补角相等求出∠DCP=∠FCP，根据SAS证出△PCF≌△PCE即可。