题目内容
【题目】如图,直线y=-![]() x+1与x轴.y轴分别交于A.B两点,抛物线y=-
x+1与x轴.y轴分别交于A.B两点,抛物线y=-![]() x2+bx+c经过点B,且与直线AB的另一交点为C(4,n).
x2+bx+c经过点B,且与直线AB的另一交点为C(4,n).
(1)求n的值及该抛物线所对应的函数关系式;
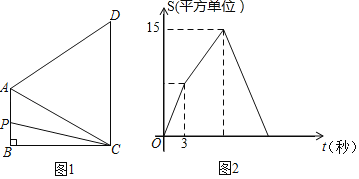
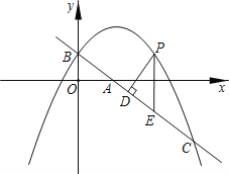
(2)设抛物线上的一个动点P的横坐标为t(0<t<4),过点P作PD⊥AB于点D,作PE∥y轴交直线AB于点E,
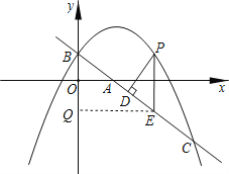
①y轴上存在点Q,使得四边形QEPB是矩形,请求出点Q的坐标;
②求线段PD的长的最大值;
③当t为何值时,点D为BE的中点.
【答案】(1)n=-2;y=![]() x2+
x2+![]() x+1;(2)①点Q的坐标为
x+1;(2)①点Q的坐标为![]() ;②PD最大=
;②PD最大=![]() ;③当t=
;③当t=![]() 时,E为BE的中点.
时,E为BE的中点.
【解析】
(1)把x=4.y=n代入![]() 中,即可求出n的值,从而求出
中,即可求出n的值,从而求出![]() 中b,c的值;
中b,c的值;
(2)①由P点的横坐标为t,则可知P点的纵坐标为![]() ,E点的坐标为
,E点的坐标为![]() ,而四边形BPEQ为矩形,点B的坐标为(0,1),则可求得
,而四边形BPEQ为矩形,点B的坐标为(0,1),则可求得![]() ,解得t值;
,解得t值;
②易证△PED∽△EBQ,则有![]() ,PD=
,PD=![]() ,得出关于t的二次函数,即可求最大值;
,得出关于t的二次函数,即可求最大值;
③点D为BE的中点,即DE=![]() BE,代入②中
BE,代入②中![]() ,即求得此时的t值.
,即求得此时的t值.
(1)把x=4.y=n代入![]() 中,得:n=
中,得:n=![]() ×4+1=-2
×4+1=-2
∴点C的坐标为(4,-2)
将点C(4,-2)和(0,1)代入![]() ,得:-8+4b+1=-2
,得:-8+4b+1=-2
解得:b=![]()
∴y=![]() x2+
x2+![]() x+1
x+1
(2)①∵P点的横坐标为t,则P点的纵坐标为![]() ,E点的纵坐标为
,E点的纵坐标为![]() ,
,
∵四边形BPEQ为矩形,故PB⊥y轴
∵点B的坐标为(0,1)
∴![]() ,
,
解得:t1=0(舍去),t2=![]()
∴t=![]() ,
,
则点E的纵坐标为:![]()
∴点Q的坐标为![]()
②∵PE=![]() t2+
t2+![]() t+1﹣(﹣
t+1﹣(﹣![]() t+1)=
t+1)=![]()
QE=t
QB=![]()
BE=![]() =
=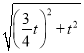 =
=![]()
∵∠BQE=∠PDE=90°
∠PEB=∠EBQ
∴△PED∽△EBQ
∴![]() ,得
,得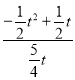 =
=![]()
PD=![]()
∵![]()
∴PD有最大值
PD最大=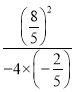 =
=![]()
③∵点D为BE的中点
∴由![]() ,DE=
,DE=![]() BE,得
BE,得![]()
代入得![]() =
=![]()
整理得,![]() 25t=-12t2+48t
25t=-12t2+48t
解得t1=0(舍去),t2=![]()
∴当t=![]() 时,E为BE的中点
时,E为BE的中点

【题目】某班“数学兴趣小组”对函数y=﹣x2+2|x|+1的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x | … | ﹣3 | ﹣ | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | ﹣2 | ﹣ | m | 2 | 1 | 2 | 1 | ﹣ | ﹣2 | … |
其中,m= .
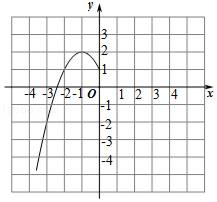
(2)根据上表数据,在如图所示的平面直角坐标系中描点,画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出两条函数的性质.
(4)进一步探究函数图象发现:
①方程﹣x2+2|x|+1=0有 个实数根;
②关于x的方程﹣x2+2|x|+1=a有4个实数根时,a的取值范围是 .
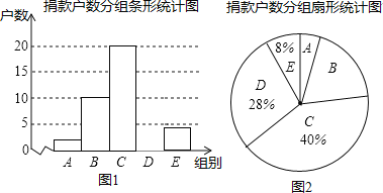
【题目】某社区组织“献爱心”捐款活动,并对部分捐款户数进行调查和分组统计,数据整理成如下统计图表(图中信息不完整).
捐款户数分组统计表
组别 | 捐款额(x)元 | 户数 |
A | 1≤x<100 | 2 |
B | 100≤x<200 | 10 |
C | 200≤x<300 | c |
D | 300≤x<400 | d |
E | x≥400 | e |
请结合以上信息解答下列问题:
(1)本次调查的样本容量是______;
(2)d=______,并补全图1;
(3)图2中,“B”所对应扇形的圆心角为______度;
(4)若该社区有500户住户,根据以上信息估计全社区捐款不少于300元的户数是______.