题目内容
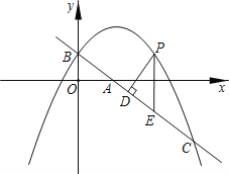
【题目】如图，在
中，
，
，取边
上一点
，连结
，
是延长线上一点，连结
并延长，交
延长线于点
．
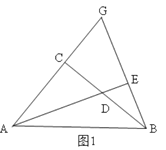
（1）如图1，若
，
，
，求
的长；
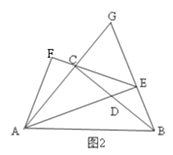
（2）如图2，连结
，过点
作
交延长线于点
，且
．求证：
．
【答案】（1）
；（2）见解析
【解析】
（1）想求
的长，由于
是直角三角形，可用解直角三角形的方法求解，因为
，
是等腰直角三角形，根据图形中角之间的关系可以得到
，那么在
中，
三边既有和差关系，又有倍数关系，这种情况可设
为
，则
为
，
，根据勾股定理列出方程，解之即可.
（2）证明线段之间的和倍关系，基本思路是通过证线段相等进行等量代换，将间接关系转化为直接关系.本题可过
作
，交于
，先通过条件
证明
为等腰直角三角形，得到
和
；下一步通过证明
得到
，将
分成
即可.
解:（1）∵
，
∴
，
∵
∴
∴
，
∵
∴
∴
∴
∴
，
设为，则为，
∵
∴
解得
∴
解得
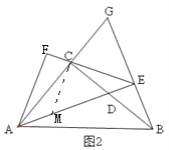
⑵证明：过作，交于
∴
∵
∴
∵
∴
∵
∴
∴
∴
∵
∴
∵
∴
∴
∴
在
中
∵
∴
．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
