Question

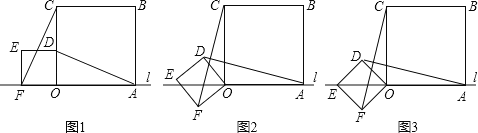
【题目】如图，正方形ABCD，EFGH的边长都等于1，点E恰好是AC，BD的交点，求两个正方形的重叠部分(阴影部分)的面积．

Answer 1

【答案】

【解析】

证明△EDP≌△ECQ，即可求得△EDP和△ECQ的面积相等，从而可证明重合部分的面积为正方形面积的.

据正方形的性质可知∠EDP=∠ECQ=45°，ED=EC.

∵∠DEP+∠CEP=90°，∠CEQ+∠CEP=90°，

∴∠DEP=∠CEQ.

在△EDP和△ECQ中，

∵EDP=∠ECQ，

ED=EC，

∠DEP=∠CEQ，

∴△EDP≌△ECQ（ASA），

∴S△EDP=S△ECQ．

∴重叠部分的面积等于△DEC的面积，

∵正方形ABCD、EFGH的边长都等于1，

∴正方形ABCD、EFGH的面积等于1，

∴重合部分的面积为.