题目内容

【题目】等腰三角形的一条高与一腰的夹角为40°，则等腰三角形的一个底角为_____．

【答案】50°或65°或25°

【解析】

分高为底边上的高和腰上的高两种情况，腰上的高再分是锐角三角形和钝角三角形两种情况讨论求解．

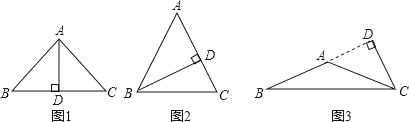
解：如图1，高为底边上的高时，∵∠BAD＝40°，

∴顶角∠BAC＝2∠BAD＝2×40°＝80°，

底角为（180°﹣80°）÷2＝50°；

高为腰上的高时，如图2，若三角形是锐角三角形，

∵∠ABD＝40°，

∴顶角∠A＝90°﹣40°＝50°，

底角为（180°﹣50°）÷2＝65°；

如图3，若三角形是钝角三角形，

∵∠ACD＝40°，

∴顶角∠BAC＝∠ACD+∠D＝40°+90°＝130°，

底角为（180°﹣130°）÷2＝25°．

综上所述，等腰三角形的一个底角为50°或65°或25°．

故答案为：50°或65°或25°．

练习册系列答案
相关题目

【题目】如图，正方形ABCD，EFGH的边长都等于1，点E恰好是AC，BD的交点，求两个正方形的重叠部分(阴影部分)的面积．

【题目】已知，如图，AB是⊙O的直径，点C为⊙O上一点，OF⊥BC于点F，交⊙O于点E，AE与BC交于点H，点D为OE的延长线上一点，且∠ODB=∠AEC．

（1）求证：BD是⊙O的切线；

（2）求证：CE2=EHEA；

（3）若⊙O的半径为5，sinA=，求BH的长．

【题目】如图，在平面直角坐标系中，半径为1个单位长度的半圆O1，O2，O3，…组成一条平滑曲线，点P从点O出发，沿这条曲线向右运动，速度为每秒 个单位长度，则第2016秒时，点P的坐标是（　　）

A.（2015,0）B.（2015，-1）C.（2016,0）D.（2016，-1）

【题目】已知：如图，在长方形ABCD中，AB=4，AD=6．延长BC到点E，使CE=2，连接DE，动点P从点B出发，以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动，设点P的运动时间为t秒，当t的值为_____秒时，△ABP和△DCE全等．

【题目】仔细阅读下面例题，解答问题：例题: 已知二次三项式x2 4x m 有一个因式是 ( x 3) ，求另一个因式以及 m 的值.

解：设另一个因式为 ( x n) ，得x2 4x m ( x 3) ( x n)

则x2 4 x m x2 (n 3) x 3n

∴

解得： n 7, m 21

∴ 另一个因式为 ( x 7) ， m 的值为－21 .

问题：仿照以上方法解答下面问题：

（1）已知二次三项式2x2+3x-k有一个因式是（2x-5），求另一个因式以及k的值．
（2）已知二次三项式6x2+4ax+2有一个因式是（2x+a），a是正整数，求另一个因式以及a的值．

【题目】如图是我国某海域内的一个小岛，其平面图如图甲所示，小明据此构造出该岛的一个数学模型如图乙所示，其中∠B＝∠D＝90°，AB＝BC＝15千米，CD＝3千米，请据此解答如下问题：

(1)求该岛的周长和面积；(结果保留整数，参考数据：≈1.414，≈1.732，≈2.449)

(2)求∠ACD的余弦值．

【题目】如图，在平面直角坐标系中，四边形ABCD是平行四边形，AD=6，若OA、OB的长是关于x的一元二次方程x2﹣7x+12=0的两个根，且OA＞OB．

（1）求A、B的坐标．

（2）求证：射线AO是∠BAC的平分线．

（3）若点M在平面直角坐标系内，则在直线AB上是否存在点F，使以A、C、F、M为顶点的四边形为菱形？若存在，直接写出F点的坐标，若不存在，请说明理由．

【题目】某公司计划从甲、乙两种产品中选择一种生产并销售，每年产销 x 件，已知产销两种产品的有关信息 如下：

产品

每件售价/万元

每件成本/万元

年最大产销量/件

甲

6

3

200

乙

20

10

80

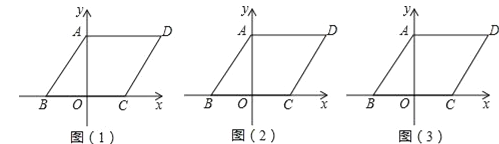
甲、乙两产品每年的其他费用与产销量的关系分别是： y1 kx b 和 y2 ax2 m ，它们的函数图象分别如图（1）和图（2）所示.

（1）求： y1 、 y2 的函数解析式；

（2）分别求出产销两种产品的最大利润；（利润=销售额-成本-其它费用）

（3）若通过技术改进，甲产品的每件成本降到 a 万元，乙产品的年最大产销量可以达到 110 件，其它都不变，为获得最大利润，该公式应该选择产销哪种产品？请说明理由.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网