Question

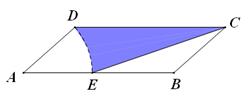
如图，AB是⊙O的一条弦，OD⊥AB，垂足为C，交⊙O于点D,点E在⊙O上．

（1）若∠AOD=52°，求∠DEB的度数；
（2）若OC=3，OA=5，求AB的长．

Answer 1

(1)26°;(2)8.

试题分析：(1)垂直于弦的直径平分弦,并且平分弦所对的弧,同弧或等弧所对的圆周角相等,同弧所对的圆
周角是圆心角的一半,由题OD⊥AB，有弧AD=弧BD ,因为∠AOD=52°，所以弧BD 所对的圆周角也是52°，
所以∠DEB=26°;(2)因为OD⊥AB，所以OD平分弦AB,即AC=BC,在Rt△AOC中，OC="3" ，AO=5,由勾股定理,AC=4,
所以AB=2AC=8.
试题解析：（1）∵OD⊥AB，垂足为C，交⊙O于点D，
∴弧AD=弧BD，
∵∠AOD=52°，
∴∠DEB=26°.
（2）∵OD⊥AB，
∴OD平分弦AB,
即AC=BC,
在Rt△AOC中，OC="3" ，AO=5,
由勾股定理, AC=4,
∴AB=2AC=8.