ĢāÄæÄŚČŻ
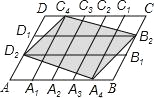
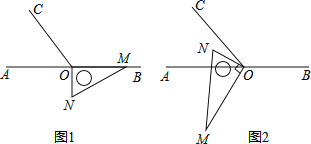
”¾ĢāÄæ”æijÖĘŌģĘóŅµÓŠŅ»×ł¶ŌÉś²śÉč±ø½ųŠŠĖ®Ń»·ĄäČ“µÄĄäČ“Ėž£¬ĄäČ“ĖžµÄ¶„²æÓŠŅ»øö½ųĖ®æŚ£¬3Š”Ź±Ē”ŗĆæÉŅŌ×¢ĀśÕā׳æÕĖž£¬µ×²æÓŠŅ»øö³öĖ®æŚ£¬7Š”Ź±Ē”ŗĆæÉŅŌ·ÅĶźĀśĖžµÄĖ®£®ĪŖĮĖ±£Ö¤°²Č«£¬ĖžÄŚŹ£ÓąĖ®Įæ²»µĆÉŁÓŚČ«ĖžĖ®ĮæµÄ ![]() £¬³öĖ®æŚŅ»Ö±“ņæŖ£¬±£Ö¤Ė®µÄŃ»·£¬½ųĖ®æŚøł¾ŻĖ®Ī»Ēéæö¶ØŹ±¶ŌĄäČ“Ėž½ųŠŠ²¹Ė®£®¼ŁÉčĆæ“ĪĒ”ŗĆŌŚŹ£ÓąĖ®ĮæĪŖĀśĖ®ĮæµÄm±¶Ź±æŖŹ¼²¹Ė®£¬²¹Āśŗó¹Ų±Õ½ųĖ®æŚ£®
£¬³öĖ®æŚŅ»Ö±“ņæŖ£¬±£Ö¤Ė®µÄŃ»·£¬½ųĖ®æŚøł¾ŻĖ®Ī»Ēéæö¶ØŹ±¶ŌĄäČ“Ėž½ųŠŠ²¹Ė®£®¼ŁÉčĆæ“ĪĒ”ŗĆŌŚŹ£ÓąĖ®ĮæĪŖĀśĖ®ĮæµÄm±¶Ź±æŖŹ¼²¹Ė®£¬²¹Āśŗó¹Ų±Õ½ųĖ®æŚ£®
£Ø1£©µ±m= ![]() Ź±£¬ĒėĪŹ£ŗĮ½“Ī²¹Ė®Ö®¼äĻąøō¶ą³¤Ź±¼ä£æĆæ“Ī²¹Ė®ŠčŅŖ¶ą³¤Ź±¼ä£æ
Ź±£¬ĒėĪŹ£ŗĮ½“Ī²¹Ė®Ö®¼äĻąøō¶ą³¤Ź±¼ä£æĆæ“Ī²¹Ė®ŠčŅŖ¶ą³¤Ź±¼ä£æ
£Ø2£©ÄÜ·ńÕŅµ½ŹŹµ±µÄmÖµ£¬Ź¹µĆĮ½“Ī²¹Ė®µÄ¼äøōŹ±¼äŗĶĆæ“ĪµÄ²¹Ė®Ź±¼äŅ»Ńł³¤£æČē¹ūÄÜ£¬ĒėĒó³ömÖµ£»Čē¹ū²»ÄÜ£¬ĒėÄć·ÖĪöĮ½“Ī²¹Ė®µÄ¼äøōŹ±¼äŗĶĆæ“ĪµÄ²¹Ė®Ź±¼äÖ®¼äµÄŹżĮæ¹ŲĻµ£¬²¢±ķŹ¾³öĄ“£®
”¾“š°ø”æ
£Ø1£©½ā£ŗÉčĮ½“Ī²¹Ė®Ö®¼äĻąøōxŠ”Ź±£¬Ćæ“Ī²¹Ė®ŠčŅŖyŠ”Ź±£¬ĀśĖžĖ®Įæ¼ĒĪŖ1£¬½ųĖ®ĖŁ¶ČĪŖ ![]() £¬³öĖ®ĖŁ¶ČĪŖ
£¬³öĖ®ĖŁ¶ČĪŖ ![]() £¬
£¬
øł¾ŻĢāŅā£¬µĆ ![]() x+
x+ ![]() =1£¬½āµĆx=
=1£¬½āµĆx= ![]() £®
£®
![]() y©
y© ![]() y+
y+ ![]() =1£¬½āµĆy=
=1£¬½āµĆy= ![]() £®
£®
“š£ŗĮ½“Ī²¹Ė®Ö®¼äĻąøō ![]() Š”Ź±£¬Ćæ“Ī²¹Ė®ŠčŅŖ
Š”Ź±£¬Ćæ“Ī²¹Ė®ŠčŅŖ ![]() Š”Ź±
Š”Ź±
£Ø2£©½ā£ŗ”ßĮ½“Ī²¹Ė®¼äøōŹ±¼ät1=£Ø1©m£©”Ā ![]() =7£Ø1©m£©Š”Ź±£¬
=7£Ø1©m£©Š”Ź±£¬
Ćæ“ĪµÄ²¹Ė®Ź±¼äĪŖ£ŗt2=£Ø1©m£©”Ā£Ø ![]() ©
© ![]() £©=
£©= ![]() £Ø1©m£©Š”Ź±£¬
£Ø1©m£©Š”Ź±£¬
”ąt1”Łt2£¬
¼“²»ÄÜÕŅµ½ŹŹµ±µÄmÖµ£¬Ź¹µĆĮ½“Ī²¹Ė®µÄ¼äøōŹ±¼äŗĶĆæ“ĪµÄ²¹Ė®Ź±¼äŅ»Ńł³¤£¬
ӧ ![]() =
= ![]() £¬
£¬
”ąĮ½“Ī²¹Ė®µÄ¼äøōŹ±¼äŗĶĆæ“ĪµÄ²¹Ė®Ź±¼äÖ®±ČĪŖ4£ŗ3
”¾½āĪö”æ£Ø1£©ÉčĮ½“Ī²¹Ė®Ö®¼äĻąøōxŠ”Ź±£¬Ćæ“Ī²¹Ė®ŠčŅŖyŠ”Ź±£¬ĀśĖžĖ®Įæ¼ĒĪŖ1£®ÓÉĄäČ“ĖžµÄ¶„²æÓŠŅ»øö½ųĖ®æŚ£¬3Š”Ź±Ē”ŗĆæÉŅŌ×¢ĀśÕā׳æÕĖžæÉÖŖ½ųĖ®ĖŁ¶ČĪŖ ![]() £¬ÓɵײæÓŠŅ»øö³öĖ®æŚ£¬7Š”Ź±Ē”ŗĆæÉŅŌ·ÅĶźĀśĖžµÄĖ®æÉµĆ³öĖ®ĖŁ¶ČĪŖ
£¬ÓɵײæÓŠŅ»øö³öĖ®æŚ£¬7Š”Ź±Ē”ŗĆæÉŅŌ·ÅĶźĀśĖžµÄĖ®æÉµĆ³öĖ®ĖŁ¶ČĪŖ ![]() £¬øł¾ŻĢāŅāĮŠ³ö·½³Ģ£¬Ēó½ā¼“æÉ£»£Ø2£©ĻČ¼ĘĖćĮ½“Ī²¹Ė®µÄ¼äøōŹ±¼ä¾ĶŹĒ³öĖ®æŚ·Å³öŅ»¶ØµÄĖ®Įæ»¹ÓąĀśĖ®ĮæµÄm±¶Ź±ĖłÓƵď±¼ä£¬ĮŠŹ½ĪŖ£ŗt1=£Ø1©m£©”Ā
£¬øł¾ŻĢāŅāĮŠ³ö·½³Ģ£¬Ēó½ā¼“æÉ£»£Ø2£©ĻČ¼ĘĖćĮ½“Ī²¹Ė®µÄ¼äøōŹ±¼ä¾ĶŹĒ³öĖ®æŚ·Å³öŅ»¶ØµÄĖ®Įæ»¹ÓąĀśĖ®ĮæµÄm±¶Ź±ĖłÓƵď±¼ä£¬ĮŠŹ½ĪŖ£ŗt1=£Ø1©m£©”Ā ![]() £¬ŌŁ¼ĘĖćĆæ“ĪµÄ²¹Ė®Ź±¼äĪŖ£ŗt2=£Ø1©m£©”Ā£Ø
£¬ŌŁ¼ĘĖćĆæ“ĪµÄ²¹Ė®Ź±¼äĪŖ£ŗt2=£Ø1©m£©”Ā£Ø ![]() ©
© ![]() £©£¬ĖłŅŌt1”Łt2 £¬ Ļą±ČŗóµĆ
£©£¬ĖłŅŌt1”Łt2 £¬ Ļą±ČŗóµĆ ![]() =
= ![]() £¬Ōņ3t1=4t2 £®
£¬Ōņ3t1=4t2 £®

 ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø
ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø”¾ĢāÄæ”æĪŖĮĖ½āijŹŠŹŠĆń”°ĀĢÉ«³öŠŠ”±·½Ź½µÄĒéæö£¬Ä³Š£ŹżŃ§ŠĖȤŠ”×éŅŌĪŹ¾ķµ÷²éµÄŠĪŹ½£¬Ė껜µ÷²éĮĖijŹŠ²æ·Ö³öŠŠŹŠĆńµÄÖ÷ŅŖ³öŠŠ·½Ź½£Ø²ĪÓėĪŹ¾ķµ÷²éµÄŹŠĆń¶¼Ö»“ÓŅŌĻĀĪåøöÖÖĄąÖŠŃ”ŌńŅ»Ąą£©£¬²¢½«µ÷²é½į¹ū»ęÖĘ³ÉČēĻĀ²»ĶźÕūµÄĶ³¼ĘĶ¼£®
ÖÖĄą | A | B | C | D | E |
³öŠŠ·½Ź½ | ¹²Ļķµ„³µ | ²½ŠŠ | ¹«½»³µ | µÄŹæ | Ė½¼Ņ³µ |

øł¾ŻŅŌÉĻŠÅĻ¢£¬»Ų“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©²ĪÓė±¾“ĪĪŹ¾ķµ÷²éµÄŹŠĆń¹²ÓŠ ČĖ£¬ĘäÖŠŃ”ŌńBĄąµÄČĖŹżÓŠ ČĖ£»
£Ø2£©ŌŚÉČŠĪĶ³¼ĘĶ¼ÖŠ£¬ĒóAĄą¶ŌÓ¦ÉČŠĪŌ²ŠÄ½Ē¦ĮµÄ¶ČŹż£¬²¢²¹Č«ĢõŠĪĶ³¼ĘĶ¼£»
£Ø3£©øĆŹŠŌ¼ÓŠ12ĶņČĖ³öŠŠ£¬Čō½«A£¬B£¬CÕāČżĄą³öŠŠ·½Ź½¾łŹÓĪŖ”°ĀĢÉ«³öŠŠ”±·½Ź½£¬Ēė¹Ą¼ĘøĆŹŠ”°ĀĢÉ«³öŠŠ”±·½Ź½µÄČĖŹż£®