题目内容
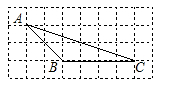
如图,在四边形ABCD中,∠DAB=60º,AC平分∠DAB,BC⊥AC,AC与BD交于点E,AD=6,CE=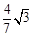 ,
,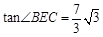 ,求BC、DE的长及四边形ABCD的面积.
,求BC、DE的长及四边形ABCD的面积.
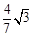 ,
,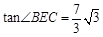 ,求BC、DE的长及四边形ABCD的面积.
,求BC、DE的长及四边形ABCD的面积.
4,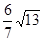 ,
,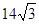
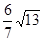 ,
,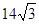
试题分析:过点D作DF⊥AC于F,先根据角平分线的性质求得∠DAC=∠BAC=30°,根据垂直的定义可得∠AFD=∠ACB=90°,再根据含30°角的直角三角形的性质即可求得DF的长,根据
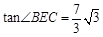 即可求得BC、EF的长,然后根据勾股定理可以求得DE的长,最后由
即可求得BC、EF的长,然后根据勾股定理可以求得DE的长,最后由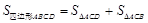 即可求得结果.
即可求得结果.过点D作DF⊥AC于F
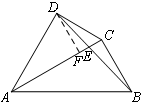
∵∠DAB=60º,AC平分∠DAB,
∴∠DAC=∠BAC=30°.
∵
 ,
,∴∠AFD=∠ACB=90°.
∴
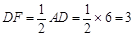 ,BC=CE
,BC=CE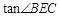 =
=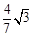
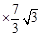 =4.
=4. ∴
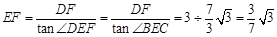 .
.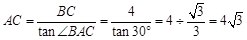 .
.∴
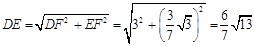 .
.∴
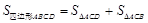
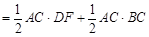
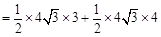
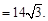
点评:此类问题知识点较多,综合性较强,在中考中比较常见,一般难度不大,需熟练掌握.

练习册系列答案
相关题目

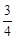 ,则BC的长 .
,则BC的长 .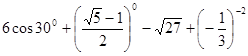
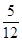
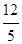
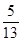
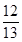
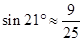 ,
,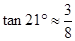 )
)