Question

【题目】如图，等腰△ABC中，AB=AC，BC∥x轴，点A．C在反比例函数y=（x＞0）的图象上，点B在反比例函数y=（x＞0）的图象上，则△ABC的面积为　 ． 　

Answer 1

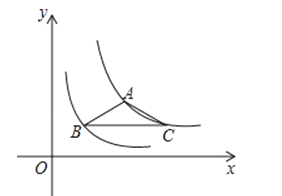
【答案】
【解析】解：作AD⊥BC于D，如图，设B（t，），
∵AB=AC，BC∥x轴，
∴BD=CD，AD∥y轴，
∴C点的纵坐标为 ，
当y=时，= ， 解得x=4t，则C点坐标为（4t，），
∴D点坐标为（t，），
∴A点的横坐标为t，
当x=t时，y== ， 则A点坐标为（t，），
∴S△ABC=（4t﹣t）（﹣）= ．
故答案为 ．

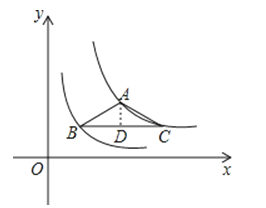
作AD⊥BC于D，如图，利用反比例函数图象上点的坐标特征，可设B（t，），根据等腰三角形的性质得BD=CD，则C点的纵坐标为 ， 于是可表示出C点坐标为（4t，），利用线段中点坐标公式表示出D点坐标为（t，），接着表示出A点坐标为（t，），然后根据三角形面积公式求解．