题目内容
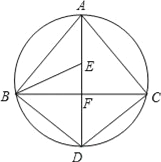
【题目】如图,在矩形ABCD中,BC=10,对角线AC与BD相交于点O,CE⊥BD,垂足为E,BE=3DE,求CE的长.
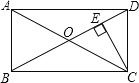
【答案】5.
【解析】
由矩形的性质得出OC=OB=OD,得出∠OBC=∠OCB,由已知条件得出OE=DE,∠BEC=90°,由线段垂直平分线的性质得出OC=CD,得出△OCD为等边三角形,因此∠OCD=60°,由三角形的外角性质得出∠EBC=30°,由含30°角的直角三角形的性质即可得出CE的长.
解:∵四边形ABCD是矩形,
∴OC=![]() AC,OB=
AC,OB=![]() BD,AC=BD,
BD,AC=BD,
∴OC=OB=OD,
∴∠OBC=∠OCB,
∵CE⊥BD,BE=3ED,
∴OE=DE,∠BEC=90°,
∴OC=CD,
∴OC=OD=CD,
∴△OCD为等边三角形,
∴∠OCD=60°,
∴∠EBC=30°,
∴CE=![]() BC=
BC=![]() ×10=5.
×10=5.

练习册系列答案
相关题目