��Ŀ����
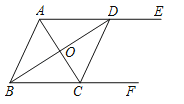
����Ŀ����ͼ1����������ABCD�У���PΪAD�ӳ�����һ�㣬����AC��CP������C��CF��CP����C����AB�ڵ�F������B��BM��CF�ڵ�N����AC�ڵ�M��
��1����AP=![]() AC��BC=4����S��ACP��
AC��BC=4����S��ACP��
��2����CP��BM=2FN����֤��BC=MC��
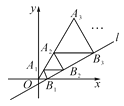
��3����ͼ2���������������������£�����������ABCD����Ϊ������ABCD������AB��BC��AC=AP��ȡCP�е�E������EB����AC�ڵ�O�����룺��AOB����ABM֮���к�������ϵ����˵�����ɣ�
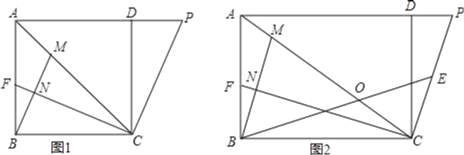
���𰸡���1��7![]() ����2��֤������������3����AOB=3��ABM�����ɼ�������
����2��֤������������3����AOB=3��ABM�����ɼ�������
��������
��1���������ε����ʵó�AB=BC=CD=4����ADC=��CDP=��ABC=��BCD=90�����ɹ��ɶ������AC���ó�AP���������S��ACP��
��2����CF�Ͻ�ȡNG=FN������BG����CF��CG=2FN��֤����BCF=��DCP����ASA֤����BCF�ա�DCP���ó�CF=CP��֤��CG=BM����SAS֤����ABM�ա�BCG���ó���AMB=��BGC�������BMC=��BGF�����߶δ�ֱƽ���ߵ����ʵó�BF=BG���ó���BFG=��BGF�������BMC=��CBM�����ɵó����ۣ�
��3������AE����֤����BCA=2��PAE����֤��A��D��E��C�ĵ㹲Բ����Բ�ܽǶ����ó���DCP=��PAE���ó���BCF=��PAE��֤����BCA=2��ABM��Ȼ���������ε�������ʼ��ɵó����ۣ�
�⣺��1�����ı���ABC�������Σ�
��AD��BC��AB=BC=CD=4����ADC=��CDP=��ABC=��BCD=90����
��AC=![]() =4
=4![]() ��
��
��AP=![]() AC=
AC=![]() ��4
��4![]() =
=![]() ��
��
��S��ACP=![]() AP��CD=
AP��CD=![]() ��
��![]() ��4=7
��4=7![]() ��
��
��2����CF�Ͻ�ȡNG=FN������BG����ͼ1��ʾ��
��CF��CG=2FN��
��CF��CP��
���PCF=90����
���BCF=��DCP��
����BCF����DCP�� ��
��
���BCF�ա�DCP��ASA����
��CF=CP��
��CP��BM=2FN��
��CG=BM��
�ߡ�ABC=90����BM��CF��
���ABM=��BCG����BFG=��CBM��
����ABM����BCG�� ��
��
���ABM�ա�BCG��SAS����
���AMB=��BGC��
���BMC=��BGF��
��GN=FN��BM��CF��
��BF=BG��
���BFG=��BGF��
���BMC=��CBM��
��BC=MC��
��3����AOB=3��ABM���������£�
����AE����ͼ2��ʾ��
��AC=AP��E��CP���е㣬
��AE��CP����PAE=��CAE��
��AD��BC��
���BCA=��PAC=2��PAE��
��CF��CP��
���PCF=90����
���BCF=��DCP��
�ߡ�ADC=��AEC=90����
��A��D��E��C�ĵ㹲Բ��
���DCP=��PAE��
���BCF=��PAE��
���ߡ�ABM=��BCF��
���ABM=��BCF=��PAE��
���BCA=2��ABM��
�ߡ�AOB=��BCF+��BCA��
���AOB=3��ABM��



 ���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�
���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�