题目内容
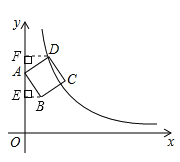
【题目】如图,边长为2的正方形ABCD的顶点A在y轴上,顶点D在反比例函数y=(x>0)的图像上,已知点B的坐标是(![]() ,
,![]() ),则k的值为( )
),则k的值为( )

A.10 B.8 C.6 D.4
【答案】B.
【解析】
试题分析:过点B作BE⊥y轴于E,过点D作DF⊥y轴于F,根据正方形的性质可得AB=AD,∠BAD=90°,再根据同角的余角相等求出∠BAE=∠ADF,然后利用“角角边”证明△ABE和△DAF全等,根据全等三角形对应边相等可得AF=BE,DF=AE,再求出OF,然后写出点D的坐标,再把点D的坐标代入反比例函数解析式计算即可求出k.具体解答过程如下,
如图,过点B作BE⊥y轴于E,过点D作DF⊥y轴于F,
在正方形ABCD中,AB=AD,∠BAD=90°,
∴∠BAE+∠DAF=90°,
∵∠DAF+∠ADF=90°,
∴∠BAE=∠ADF,
在△ABE和△DAF中,
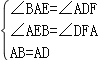 ,
,
∴△ABE≌△DAF(AAS),
∴AF=BE,DF=AE,
∵正方形的边长为2,B(![]() ,
,![]() ),
),
∴BE=![]() ,AE=
,AE=![]() ,
,
∴OF=OE+AE+AF=![]() ,
,
∴点D的坐标为(![]() ,5),
,5),
∵顶点D在反比例函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴k=xy=![]() ×5=8.
×5=8.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
【题目】2018年体育中考中,我班一学习小组6名学生的体育成绩如下表,则这组学生的体育成绩的众数,中位数依次为( )
成绩(分) | 47 | 48 | 50 |
人数 | 2 | 3 | 1 |
A. 48,48 B. 48,47.5 C. 3,2.5 D. 3,2