题目内容

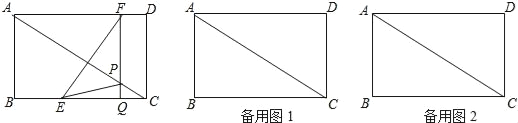
【题目】如图，在矩形ABCD中，AB=6，AD=8，点P是BC中点，点E、F是边CD上的任意两点，且EF=2，当四边形APEF的周长最小时，则DF的长为（　　）

A. 2 B. 4 C. D.

【答案】C

【解析】

如图，作P关于CD的对称点M，在AB上截取AH=2，然后连接HM交CD于E，接着在CD上截取EF=2，那么E、F两点即可满足题目要求，利用相似三角形的性质即可求出CE的长，进一步得到DF的长．

如图，作P关于CD的对称点M，在AB上截取AH=2，然后连接HM交CD于E，接着在CD上截取EF=2，那么E、F两点即可满足使四边形APEF的周长最小．

∵在矩形ABCD中，AB=6，BC=8，点P是BC中点，∴CP=CM=4，MB=12，而AH=2，∴BH=4，

∵AB∥CD，∴△CEM∽△BHM，∴CE：BH=MC：MB，∴CE==，∴DF=CD﹣CE﹣EF=6﹣﹣2=．

故选C．

练习册系列答案
相关题目

【题目】如图，在矩形ABCD中，AB=6cm，BC=8cm，如果点E由点B出发沿BC方向向点C匀速运动，同时点F由点D出发沿DA方向向点A匀速运动，它们的速度分别为每秒2cm和1cm，FQ⊥BC，分别交AC、BC于点P和Q，设运动时间为t秒（0＜t＜4）．

（1）连接EF，若运动时间t=　 　时，EF⊥AC；

（2）连接EP，当△EPC的面积为3cm2时，求t的值；

（3）若△EQP∽△ADC，求t的值．

【题目】在△ABC中，AB边的垂直平分线l1交BC于D，AC边的垂直平分线l2交BC于E，l1与l2相交于点O．△ADE的周长为6cm．

（1）求BC的长；

（2）分别连结OA、OB、OC，若△OBC的周长为16cm，求OA的长．

【题目】已知，点O是等边△ABC内的任一点，连接OA，OB，OC．

（1）如图1，已知∠AOB=150°，∠BOC=120°，将△BOC绕点C按顺时针方向旋转60°得△ADC．

①∠DAO的度数是 ；

②用等式表示线段OA，OB，OC之间的数量关系，并证明；

（2）设∠AOB=α，∠BOC=β．

①当α，β满足什么关系时，OA+OB+OC有最小值？请在图2中画出符合条件的图形，并说明理由；

②若等边△ABC的边长为1，直接写出OA+OB+OC的最小值．

【题目】如图，在Rt△ABC中，∠C=90°，AC=BC=6cm，点P 从点A 出发，沿AB方向以每秒cm的速度向终点B运动；同时，动点Q从点B出发沿BC方向以每秒1cm 的速度向终点C运动，将△PQC沿BC翻折，点P的对应点为点P′.设Q点运动的时间 t 秒，若四边形QPCP′为菱形，则 t 的值为（ ）

A. B. 2 C. 2 D. 4

【题目】已知：如图，AE⊥BC，FG⊥BC，∠1=∠2，∠D=∠3+60°，∠CBD=70°．

（1）求证：AB∥CD；

（2）求∠C的度数．

【题目】如图，AB为⊙O的直径，点D为AB下方⊙O上一点，点C为弧ABD的中点，连接CD，CA．

（1）求证：∠ABD=2∠BDC；

（2）过点C作CH⊥AB于H，交AD于E，求证：EA=EC；

（3）在（2）的条件下，若OH=5，AD=24，求线段DE的长度．

【题目】如图，△ABC中，点E在BC边上．AE=AB，将线段AC绕点A旋转到AF的位置．使得∠CAF=∠BAE.连接EF，EF与AC交于点G．

(1)求证：EF =BC；

(2)若∠ABC=65°，∠ACB=28°，求∠FGC的度数．

【题目】如图，CD是经过∠BCA顶点C的一条直线，且直线CD经过∠BCA的内部，点E，F在射线CD上，已知CA=CB且∠BEC=∠CFA=∠α．

（1）如图1，若∠BCA=80°，∠α=90°，问EF=BE-AF，成立吗？说明理由．

（2）将（1）中的已知条件改成∠BCA=∠β，∠α+∠β=180°（如图2），问EF=BE-AF仍成立吗？说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网