题目内容
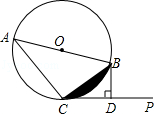
【题目】如图，AB是半圆O直径，半径OC⊥AB，连接AC，∠CAB的平分线AD分别交OC于点E，交 
于点D，连接CD、OD，以下三个结论：①AC∥OD；②AC=2CD；③线段CD是CE与CO的比例中项，其中所有正确结论的序号是（ ） 
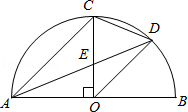
A.①②
B.①③
C.②③
D.①②③
【答案】B
【解析】解：∵OA=OD， ∴∠OAD=∠ODA，
∵AD为∠CAB的平分线，
∴∠CAD=∠OAD，
∴∠CAD=∠ODA，
∴AC∥OD，故选项①正确；
∵OC⊥AB，OA=OC，
∴△AOC为等腰直角三角形，
∴∠DOB=∠COD=∠BAC=45°，
∵∠ADC与∠AOC都对 
，
∴∠ADC= 
∠AOC=45°，
∴∠ADC=∠COD，又∠OCD=∠DCE，
∴△DCE∽△OCD，
∴ 
= 
，即CD2=CEOC，
故选项③正确；
取 的中点F，可得 
= 
，
∵ =2 
，
∴ = 
= ，
∴AF=FC=CD，即AF+FC=2CD，
∵AF+FC＞AC，
则2CD＞AC，故选项②错误，
则正确的选项有：①③．
故选B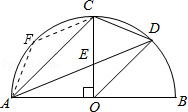
由OA=OD，利用等边对等角得到一对角相等，再由AD为角平分线得到一对角相等，等量代换得到一对内错角相等，利用内错角相等两直线平行即可得到AC与OD平行，故选项①正确；由CO垂直于AB，OA=OC，得到三角形AOC为等腰直角三角形，得到∠CAB为45度，再由两直线平行同位角相等得到∠DOB为45度，即∠COD为45度，再由同弧所对的圆周角等于圆心角的一半得到∠ADC为45度，得到一对角相等，再由一对公共角，利用两对对应角相等的两三角形相似得到三角形CED与三角形OCD相似，由相似得比例可得出CD为CE与CO的比例中项，故选项③正确；取弧AC的中点F，得到弧AF与弧CF相等，再由弧AC=2弧CD，得到三条弧相等，利用等弧对等弦得到CF=AF=CD，即CF+AF=2CD，而CF+AF大于AC，可得出AC不等式2CD，故选项②错误．
