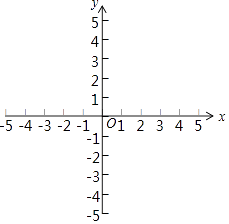Question

【题目】如图，平面直角坐标系中，平行四边形OABC的顶点C（3，4），边OA落在x正半轴上，P为线段AC上一点，过点P分别作DE∥OC，FG∥OA交平行四边形各边如图．若反比例函数 的图象经过点D，四边形BCFG的面积为8，则k的值为（ ）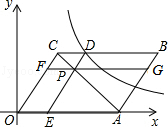
A.16
B.20
C.24
D.28

Answer 1

【答案】B
【解析】解：由图可得， SABCD ， 又∵S△FCP=S△DCP且S△AEP=S△AGP ，
∴SOEPF=SBGPD ，
∵四边形BCFG的面积为8，
∴SCDEO=SBCFG=8，
又∵点C的纵坐标是4，则CDOE的高是4，
∴OE=CD= ，
∴点D的横坐标是5，
即点D的坐标是（5，4），
∴4= ，解得k=20，
故选B．
根据图形可得，△CPF与△CPD的面积相等，△APE与△APG的面积相等，四边形BCFG的面积为8，点C（3，4），可以求得点D的坐标，从而可以求得k的值．