题目内容
如图,点O是平行四边形ABCD的对称中心,将直线DB绕点O顺时针方向旋转,交DC、AB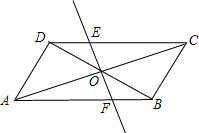 于点E、F.
于点E、F.(1)证明:△DEO≌△BFO;
(2)若DB=2,AD=1,AB=
| 5 |
①当DB绕点O顺时针方向旋转45°时,判断四边形AECF的形状,并说明理由;
②在直线DB绕点O顺时针方向旋转的过程中,是否存在矩形DEBF,若存在,请求出相应的旋转角度(结果精确到1°);若不存在,请说明理由.
分析:(1)要证三角形全等,必须找到三个条件证明其全等.
(2)首先要判断四边形是什么形状,然后根据题意首先证明△OAD是等腰直角三角形,然后证明OE=OF.
(2)首先要判断四边形是什么形状,然后根据题意首先证明△OAD是等腰直角三角形,然后证明OE=OF.
解答:(1)证明:在平行四边形ABCD中,CD∥AB,
∴∠CDO=∠ABO,∠DEO=∠BFO.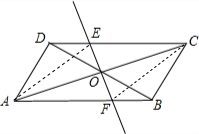
又∵点O是平行四边形的对称中心,
∴OD=OB.
∴△DEO≌△BFO.
(2)解:①四边形AECF是菱形.
理由如下:
在△ABD中,DB=2,AD=1,AB=
,
∴DB2+AD2=AB2.
∴△ABD是直角三角形,且∠ADB=90°
∵OD=OB=
DB=1,
∴AD=OD=1.
∴△OAD是等腰直角三角形,
∴∠AOD=45°.
当直线DB绕点O顺时针旋转45°时,即∠DOE=45°,
∴∠AOE=90°
∵△DEO≌△BFO,
∴OE=OF
又∵点O是平行四边形的对称中心,
∴OA=OC
∴四边形AECF是平行四边形
∴四边形AECF是菱形.
②当四边形DEBF是矩形时,
则有∠DFB=∠FDE=90°,OD=OE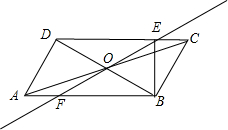
又∵∠ADB=90°
∴有∠ADF=∠ODE=∠DEO
∵S△ABD=
AD•BD=
AB•DF
∴DF=
=
=
在Rt△ADF中,cos∠ADF=
=DF=
∴∠ADF≈26.6°
∴∠ODE=∠DEO=∠ADF=26.6°
∴∠DOE=180°-∠OED-∠ODE=180°-26.6°-26.6°=126.8°≈127°
即当直线DB绕点O约顺时针旋转127°时,四边形CDBE是矩形.
∴∠CDO=∠ABO,∠DEO=∠BFO.

又∵点O是平行四边形的对称中心,
∴OD=OB.
∴△DEO≌△BFO.
(2)解:①四边形AECF是菱形.
理由如下:
在△ABD中,DB=2,AD=1,AB=
| 5 |
∴DB2+AD2=AB2.
∴△ABD是直角三角形,且∠ADB=90°
∵OD=OB=
| 1 |
| 2 |
∴AD=OD=1.
∴△OAD是等腰直角三角形,
∴∠AOD=45°.
当直线DB绕点O顺时针旋转45°时,即∠DOE=45°,
∴∠AOE=90°
∵△DEO≌△BFO,
∴OE=OF
又∵点O是平行四边形的对称中心,
∴OA=OC
∴四边形AECF是平行四边形
∴四边形AECF是菱形.
②当四边形DEBF是矩形时,
则有∠DFB=∠FDE=90°,OD=OE

又∵∠ADB=90°
∴有∠ADF=∠ODE=∠DEO
∵S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
∴DF=
| AD•BD |
| AB |
| 1×2 | ||
|
2
| ||
| 5 |
在Rt△ADF中,cos∠ADF=
| DF |
| AD |
2
| ||
| 5 |
∴∠ADF≈26.6°
∴∠ODE=∠DEO=∠ADF=26.6°
∴∠DOE=180°-∠OED-∠ODE=180°-26.6°-26.6°=126.8°≈127°
即当直线DB绕点O约顺时针旋转127°时,四边形CDBE是矩形.
点评:本题是一道综合型试题,比较难,证明三角形全等必须要找出三个条件相等,按照判定四边形形状的定义证明该四边形为何形状.

练习册系列答案
相关题目
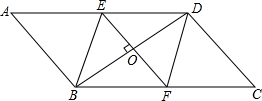 别交于点E、F.
别交于点E、F. 
 如图,在四边形ABCD中,点E、F、G、H分别是各边的中点,则按要求完成下列题目.
如图,在四边形ABCD中,点E、F、G、H分别是各边的中点,则按要求完成下列题目.
