题目内容
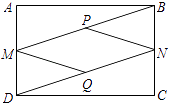
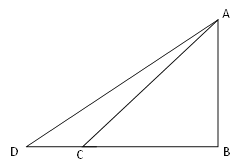
【题目】如图,在ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①∠OBE= ![]() ∠ADO;②EG=EF;③GF平分∠AGE;④EF⊥GE,其中正确的是 .
∠ADO;②EG=EF;③GF平分∠AGE;④EF⊥GE,其中正确的是 . 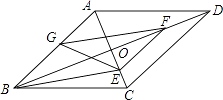
【答案】①②③
【解析】①②③解:①∵四边形ABCD是平行四边形, ∴AD∥BC,AD=BC,DO=BO= ![]() BD,
BD,
∴∠ADB=∠DBC,
∵BD=2AD,
∴AD=DO,
∴BC=BO,
∵E是CO中点,
∴∠OBE= ![]() ∠OBC,
∠OBC,
∴∠OBE= ![]() ∠ADO,故①正确;
∠ADO,故①正确;
②∵BC=BO,
∴△BOC是等腰三角形,
∵E是CO中点,
∴EB⊥CO,
∴∠BEA=90°,
∵G为AB中点,
∴EG= ![]() AB,
AB,
∵四边形ABCD是平行四边形,
∴AB=CD,
∵E、F分别是OC、OD的中点,
∴EF= ![]() CD
CD
∴EG=EF,故②正确;
③∵,E、F分别是OC、OD的中点,
∴EF∥DC,
∵DC∥AB,
∴EF∥AB,
∴∠EFG=∠AGF,
∵EF=EG,
∴∠EFG=∠EGF,
∴∠EGF=∠AGF,
∴GF平分∠AGE,故③正确;
所以答案是:①②③.
【考点精析】掌握平行四边形的性质是解答本题的根本,需要知道平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.

练习册系列答案
相关题目