题目内容
【题目】如图,已知在四边形ABCD中,AB=CD,BC=AD,E、F是对角线AC上两点,且AE=CF.求证:BE=DF.

【答案】证明见解析.
【解析】
法一可先证四边形ABCD是平行四边形,再证△ABE≌△CDF,即可证明BE=DF.法二根据先证四边形ABCD是平行四边形平行.根据SAS证△ABE≌△CDF,即可推出BE=DF.
解:法一)∵AB=CD,BC=AD,∴四边形ABCD是平行四边形
∴AB∥CD ,∴∠BAE=∠DCF
又∵AE=CF ,∴△ABE≌△CDF(SAS) ,∴BE=DF .
法二)连接BF、DE及BD,BD交AC于点O,
. 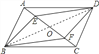
∵AB=CD,BC=AD∴四边形ABCD是平行四边形
∴OB=OD,OA=OC ∵AE=CF
∴OA-AE=OC-CF ,即OE=OF
∴△ABE≌△CDF(SAS) ,∴BE=DF.

练习册系列答案
相关题目





