题目内容
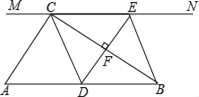
【题目】如图:在Rt△ABC中,∠ACB=90°,AB=6,过点C的直线MN∥AB,D为AB上一点,过点D作DE⊥BC,交直线MN于点E,垂足为F,连结CD,BE,
(1)当点D是AB的中点时,四边形BECD是什么特殊四边形?说明你的理由
(2)在(1)的条件下,当∠A= 时四边形BECD是正方形.
【答案】(1)当点D是AB的中点时,四边形BECD是菱形;(2)45°
【解析】试题分析:(1)先证明AC∥DE,得出四边形BECD是平行四边形,再“根据直角三角形斜边上的中线等于斜边的一半”证出CD=BD,得出四边形BECD是菱形;
(2)先求出∠ABC=45°,再根据菱形的性质求出∠DBE=90°,即可证出结论.
试题解析:(1)当点D是AB的中点时,四边形BECD是菱形;理由如下:
∵DE⊥BC,
∴∠DFB=90°,
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
∵D为AB中点,
∴AD=BD,
∴BD=CE,
∵BD∥CE,
∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,
∴CD=![]() AB=BD,
AB=BD,
∴四边形BECD是菱形;
(2)当∠A=45°时,四边形BECD是正方形;
理由如下:
∵∠ACB=90°,∠A=45°,
∴∠ABC=45°,
∵四边形BECD是菱形,
∴∠ABC=![]() ∠DBE,
∠DBE,
∴∠DBE=90°,
∴四边形BECD是正方形.
故答案为:45°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目