题目内容
12. 如图,一次函数y=x-1的图象与反比例函数y=$\frac{2}{x}$的图象相交于A(m,1),B(-1,n)两点.
如图,一次函数y=x-1的图象与反比例函数y=$\frac{2}{x}$的图象相交于A(m,1),B(-1,n)两点.(1)求m、n的值.
(2)直接写出使反比例函数值大于一次函数值的x的取值范围.
分析 (1)根据一次函数y=x-1的图象与反比例函数y=$\frac{2}{x}$的图象相交于A(m,1),B(-1,n)两点,可以求得m、n的值;
(2)根据函数图象和点A、B的坐标可以得到当x为何值时,反比例函数值大于一次函数值.
解答 解:(1)∵一次函数y=x-1的图象与反比例函数y=$\frac{2}{x}$(k≠0)的图象相交于A(m,1),B(-1,n)两点,
∴将y=1代入y=x-1得,x=2;将x=-1代入y=x-1得y=-2;
∴点A(2,1),点B(-1,-2),
∴即m的值2,n的值为-2;
(2)由函数的图象可知,当x<-1或0<x<2时,反比例函数值大于一次函数值.
点评 本题考查反比例函数和一次函数的交点问题,解题的关键是明确题意,利用数形结合的思想,找出所求问题需要的条件.

练习册系列答案
相关题目
3.随着人们生活水平的提高,家用轿车越来越多地进入家庭.王先生家中买了一辆小轿车,他连续记录了7天中每天行驶的路程(如下表),以50km为标准,多于50km的记为“+”,不足50km的记为“-”,刚好50km的记为“0”.
(1)请求出这七天中平均每天行驶多少千米?
(2)若每行驶100km需用汽油6升,汽油价5.8元/升,请估计王先生家一个月(按30天计)的汽油费用是多少元?
| 第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 | |
| 路程(km) | -8 | -11 | -14 | 0 | -16 | +41 | +8 |
(2)若每行驶100km需用汽油6升,汽油价5.8元/升,请估计王先生家一个月(按30天计)的汽油费用是多少元?
4.估计21的算术平方根的大小在( )
| A. | 2与3之间 | B. | 3与4之间 | C. | 4与5之间 | D. | 5与6之间 |
2.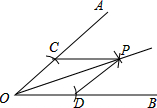 如图,用尺规作已知角平分线,其根据是构造两个三角形全等,它所用到的判别方法是( )
如图,用尺规作已知角平分线,其根据是构造两个三角形全等,它所用到的判别方法是( )
 如图,用尺规作已知角平分线,其根据是构造两个三角形全等,它所用到的判别方法是( )
如图,用尺规作已知角平分线,其根据是构造两个三角形全等,它所用到的判别方法是( )| A. | SAS | B. | ASA | C. | AAS | D. | SSS |
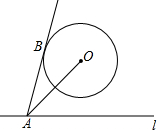 如图,点A是直线l上一点,AB切⊙O于点B,圆心O与点A间的最小距离是6cm,⊙O的半径为4cm,则AB的最小值是2$\sqrt{6}$.
如图,点A是直线l上一点,AB切⊙O于点B,圆心O与点A间的最小距离是6cm,⊙O的半径为4cm,则AB的最小值是2$\sqrt{6}$.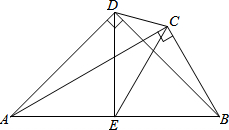 如图,在△ABC中,∠ACB=90°,以AB长为一边作△ABD,∠ADB=90°,取AB中点E,连DE、CE、CD.
如图,在△ABC中,∠ACB=90°,以AB长为一边作△ABD,∠ADB=90°,取AB中点E,连DE、CE、CD.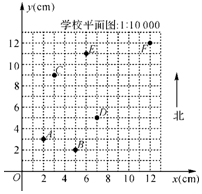 如图是某学校的平面示意图.A,B,C,D,E,F分别表示学校的第1,2,3,4,5,6号楼.
如图是某学校的平面示意图.A,B,C,D,E,F分别表示学校的第1,2,3,4,5,6号楼.