��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=a��x��1��2+4��x�ύ�ڵ�A��B���㣬��y�ύ�ڵ�C���ҵ�B������Ϊ��3��0������P�������������ϣ��Ҳ���B��C�����غϣ�����P��y��Ĵ���������BC���ڵ�Q����PQΪ����Rt��PQF��ʹ��PQF=90�㣬��F�ڵ�Q���·�����QF=1�����߶�PQ�ij���Ϊd����P�ĺ�����Ϊm��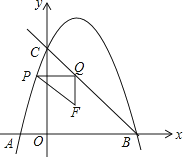
��1������������������Ӧ�ĺ�������ʽ��
��2����d��m֮��ĺ�����ϵʽ��
��3����Rt��PQF�ı�PF��y��ƽ��ʱ����d��ֵ��
��4����OBΪ��������ֱ��������OBD����0��m��3ʱ��ֱ��д����F���ڡ�OBD�ı���ʱm��ֵ��
���𰸡�
��1��
�⣺�ѵ�B��3��0������������y=a��x��1��2+4��
�ã�4a+4=0��
��ã�a=��1��
�������ߵĺ�������ʽΪ��y=����x��1��2+4=��x2+2x+3��
�������߽���ʽΪ��y=��x2+2x+3��
��2��
�⣺����������y=��x2+2x+3��
��x=0ʱ��y=3��
��y=0ʱ��x=��1����x=3��
��C��0��3����A����1��0����B��3��0����
��ֱ��BC�Ľ���ʽΪ��y=kx+b��
��������ã�![]() ��
��
��ã�k=��1��b=3��
��ֱ��BC�Ľ���ʽΪ��y=��x+3��
�ߵ�P������Ϊ����m����m2+2m+3����
���Q����������������m2+2m+3��
��x+3=��m2+2m+3��x=m2��2m��
���Q��������m2��2m����m2+2m+3����
�൱��1��m��0ʱ����ͼ1��
d=m2��2m��m=m2��3m��
��0��x��3ʱ����ͼ2��
d=m����m2��2m��=��m2+3m
��d��m֮��ĺ�����ϵʽΪ��d=![]() ��
��
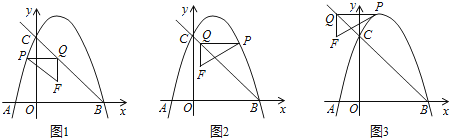
��3��
�⣺��Rt��PQF�ı�PF��y��ƽ��ʱ����P���Q����y��Գƣ�
������껥Ϊ�෴����
��m2��2m+m=0��
��ã�m=1����m=0���������⣬��ȥ����
��m=1��
��d=3��1=2��
��4��
�⣺�����������
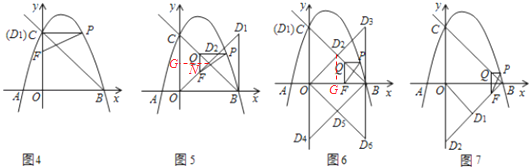
������һ����ͼ4��ʾ��
��C���������0��3����
��y=3���뺯��y=��x2+2x+3��x1=0����ȥ����x2=2��
��P������m=2��
�����ζ�����ͼ5��ʾ����D2����D2G��CO��QF��N�㣬
��B��0��3��
��D2��![]() ��
��![]() ����
����
��CO=3��QF=1��QF��CO��
��![]() =
=![]() ��
��
��D2N=![]() ��
��
��Q��1��2����
��y=2���뺯��y=��x2+2x+3��x1=![]() ��x2=
��x2=![]() ����ȥ����
����ȥ����
��m=![]() ��
��
������������ͼ6��ʾ����D2����D2G��OB��
��B��0��3��
��D2��![]() ��
��![]() ����
����
��BG=![]() ��QF=1��QF��CO��
��QF=1��QF��CO��
��![]() =
=![]() ��
��
��BF=1��
��Q��1��1����
��y=1���뺯��y=��x2+2x+3��x1=![]() ��x2=
��x2=![]() ����ȥ����
����ȥ����
��m=![]() ��
��
�������ģ���ͼ7��ʾ��
��CD2=6��QF=1��BC=![]() ����QF��CD2��
����QF��CD2��
��![]() ��
��
��BQ=![]() ��
��
��Q��������Ϊ![]() ����P�������꣬
����P�������꣬
��y=![]() ���뺯��y=��x2+2x+3��x1=
���뺯��y=��x2+2x+3��x1=![]() ��x2=
��x2=![]() ����ȥ����
����ȥ����
��m=![]() ��
��
������������0��m��3ʱ����F���ڡ�OBD�ı���ʱm��ֵΪ��2����![]() ����
����![]() ����
����![]() ��
��
����������1���ѵ�B��3��0������������y=a��x��1��2+4�����a��ֵ���ɣ�
��2�������ֱ��BC�Ľ���ʽ���ɵ�Q����������������꣬���PQ�����ɵó������
��3��������ó���P���Q����y��Գƣ��ó����̣��ⷽ�̼��ɣ�
��4��������������ٵ���F���ڡ�OBD��ֱ�DZ���ʱ���ӳ�QF��OB��G��֤����OFG�ǵ���ֱ�������Σ��ó�OG=FG����FG=QG��QF���ó����̣��ⷽ�̼��ɣ�
�ڵ���F���ڡ�OBD��б����ʱ��֤����BQF�ǵ���ֱ�������Σ��ó�BF=QF=1��OF=2���ó����̣��ⷽ�̼��ɣ�

 ��У��������ĩ��̾�ϵ�д�
��У��������ĩ��̾�ϵ�д�