Question

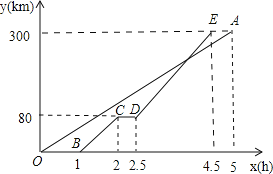
【题目】甲、乙两地距离300km，一辆货车和一辆轿车先后从甲地出发驶向乙地．如图，线段OA表示货车离甲地的距离y（km）与时间x（h）之间的函数关系，折线BCDE表示轿车离甲地的距离y（km）与时间x（h）之间的函数关系，根据图象，解答下列问题：

（1）线段CD表示轿车在途中停留了 h；

（2）求线段DE对应的函数解析式；

（3）求轿车从甲地出发后经过多长时间追上货车．

Answer 1

【答案】（1）0.5小时；（2）y=110x﹣195（2.5≤x≤4.5）；（3）轿车从甲地出发后经过2.9小时追上货车．

【解析】

试题分析：（1）利用图象得出CD这段时间为2.5﹣2=0.5，得出答案即可；

（2）利用D点坐标为：（2.5，80），E点坐标为：（4.5，300），求出函数解析式即可；

（3）利用OA的解析式得出，当60x=110x﹣195时，即可求出轿车追上货车的时间．

解：（1）利用图象可得：线段CD表示轿车在途中停留了：2.5﹣2=0.5小时；

（2）根据D点坐标为：（2.5，80），E点坐标为：（4.5，300），

代入y=kx+b，得：

，

解得：，

故线段DE对应的函数解析式为：y=110x﹣195（2.5≤x≤4.5）；

（3）∵A点坐标为：（5，300），

代入解析式y=ax得，

300=5a，

解得：a=60，

故y=60x，当60x=110x﹣195，

解得：x=3.9，故3.9﹣1=2.9（小时），

答：轿车从甲地出发后经过2.9小时追上货车．