题目内容
【题目】已知:如图,在ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.
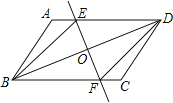
(1)求证:△DOE≌△BOF;
(2)当∠DOE等于多少度时,四边形BFDE为菱形?请说明理由.
【答案】(1)见解析;(2)∠EOD=90°,四边形BFDE为菱形.
【解析】
试题分析:(1)利用平行四边形的性质以及全等三角形的判定方法得出△DOE≌△BOF(ASA);
(2)首先利用一组对边平行且相等的四边形是平行四边形得出四边形EBFD是平行四边形,进而利用垂直平分线的性质得出BE=ED,即可得出答案.
(1)证明:∵在ABCD中,O为对角线BD的中点,
∴BO=DO,∠EDB=∠FBO,
在△EOD和△FOB中
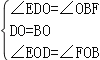 ,
,
∴△DOE≌△BOF(ASA);
(2)解:当∠DOE=90°时,四边形BFDE为菱形,
理由:∵△DOE≌△BOF,
∴OE=OF,
又∵OB=OD
∴四边形EBFD是平行四边形,
∵∠EOD=90°,
∴EF⊥BD,
∴四边形BFDE为菱形.

练习册系列答案
相关题目

