题目内容
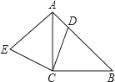
【题目】如图,已知△ABC为等腰直角三角形,D为斜边AB上任意一点,(不与点A、B重合),连接CD,作EC⊥DC,且EC=DC,连接AE,则∠EAC为_______________度.
【答案】45
【解析】
由等腰直角三角形ABC的两腰相等的性质推知AC=CB,再根据已知条件“∠ACB=∠DCE=90°”求得∠ACE=90°-∠ACD=∠DCB,然后再加上已知条件DC=EC,可以根据全等三角形的判定定理SAS判定△ACE≌△BCD;最后由全等三角形的对应角相等的性质证明结论即可.
∵△ABC是等腰直角三角形,∠ACB=90°,
∴AC=CB.
∵∠ACB=∠DCE=90°,
∴∠ACE=90°-∠ACD=∠DCB.
在△ACE和△BCD中,
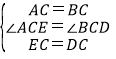 ,
,
∴△ACE≌△BCD(SAS).
∴∠B=∠EAC(全等三角形的对应角相等).
∵∠B=45°,
∴∠EAC=45°.
故答案为45°.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目