��Ŀ����
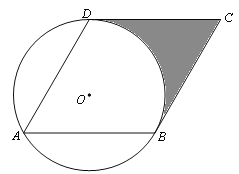
����Ŀ����ij�е��Ĵε������ϣ�����˽����������о�ʤȫ��С���ķܶ�Ŀ�꣬Ϊ��Ӧ��ί���٣�ѧУ��������У�ڵ�һС�㳡����ͼ�Ǹù㳡��ƽ��ʾ��ͼ��������6��������ƴ�ɵij����Σ���֪�м���С��������A�ı߳���1�ף� 
��1������ͼ�����������B�ı߳���x�ף����ú�x�Ĵ���ʽ�ֱ��ʾ��������F��E��C�ı߳���
��2���۲�ͼ�ε��ص��֪����������Ե���������ȵģ���ͼ�е�MN��PQ������������������ϵ�����x��ֵ��
��3�������ų����ι㳡��������������ˮ�ܵ����ɼס���2�����̶ӵ�������ֱ���Ҫ10�졢15����ɣ����Ӻ���ʩ��2�����������������µĹ������Ҷӵ���ʩ�������ʻ�Ҫ��������ɣ�
���𰸡�
��1���⣺��ͼ�����������B�ı߳���x�ף�
����С�������εı߳���1�ף�
��������F�ı߳�Ϊ��x��1���ף�������E�ı߳�Ϊ��x��2���ף�������C�ı߳�Ϊ��x��3���� ![]() ��
��
��2���⣺��MQ=PN��
��x��1+x��2=x+ ![]() ��
��
��ã�x=7��
��x��ֵΪ7
��3���⣺�����µĹ������Ҷӵ���ʩ������Ҫy����ɣ�
���������� ![]() +
+ ![]() ����2+
����2+ ![]() y=1��
y=1��
��ã�y=10��
�����µĹ������Ҷӵ���ʩ������Ҫ10�����
����������1����ͼ�����������B�ı߳���x�ף�����ͼ���и������α���ߵĹ�ϵ�����С�������εı߳���1�ף������ҳ�������F��E��C�ı߳�����2�����������ε����ʼ��ɵó�MQ=PN���ɴ˼��ɵó�����x��һԪһ�η��̣���֮���ɵó����ۣ���3�������µĹ������Ҷӵ���ʩ������Ҫy����ɣ����ݹ�������=����ʱ�������Ч�ʼ����г�����y��һԪһ�η��̣���֮���ɵó����ۣ�

 ��ѧȫ��������ѵ��ϵ�д�
��ѧȫ��������ѵ��ϵ�д�