��Ŀ����
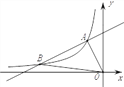
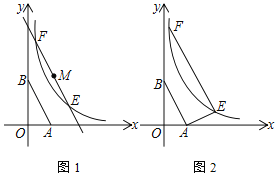
����Ŀ����ͼ1��A��1��0����B��0��2����˫����y��![]() ��x��0��
��x��0��
��1�������߶�AB��A��˳ʱ����ת90����B�Ķ�Ӧ��ǡ������˫����y��![]() ��x��0����
��x��0����
����k��ֵΪ�� ��
�ڽ�ֱ��ABƽ����˫����y��![]() ��x��0������E��F��EF���е�ΪM��a��b������
��x��0������E��F��EF���е�ΪM��a��b������![]() ��ֵ��
��ֵ��
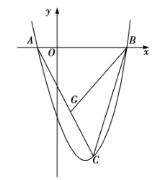
��2����ֱ��ABƽ����˫����y��![]() ��x��0������E��F������AE����AB��AE����EF��2AB����ͼ2��ֱ��д��k��ֵ�� ��
��x��0������E��F������AE����AB��AE����EF��2AB����ͼ2��ֱ��д��k��ֵ�� ��
���𰸡���1����k��3����2����2��k��![]() ��
��
��������
��1�������A��B������꣬�������ת��B������꣬�����ɴ���ϵ�������k��ɣ�
��2�����EF�Ľ���ʽ���������E��F�����꣬���е����깫ʽ���M������꣬������![]() ��
��
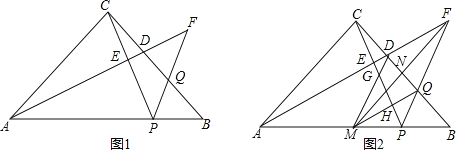
��3������ABO�ס�EHA�ã�![]() ����EH=m����AH=2m�����EF�ı���ʽ���뷴������������ʽ���������F���꣬�������
����EH=m����AH=2m�����EF�ı���ʽ���뷴������������ʽ���������F���꣬�������
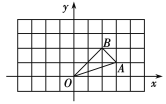
��1��������ת���B�Ķ�Ӧ��Ϊ��C������C��CD��x���ڵ�D����ͼ��ʾ
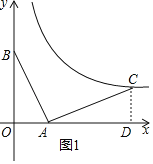
�ߡ�BAC��90����
���BAO+��CAD��90����
�ߡ�BAO+��ABO��90����
���ABO����CAD��
����OAB����DCA��
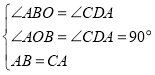 ��
��
���OAB�ա�DCA��AAS����
��CD��OA��1��
AD��OB��2��
��OD��OA+AD��3��
��C��3��1����
��C��3��1������y��![]() ����k��3��
����k��3��
�ʴ�Ϊ3��
��ֱ��AB����ʽ�е�kֵΪ��2��AB��EF����ֱ��EF����ʽ�е�kֵΪ��2��
���E��m��n����mn��3��
ֱ��EF�ı���ʽΪ��y����2x+t��
����E���������ʽ����ã�ֱ��EF�ı���ʽΪy����2x+2m+n��
��ֱ��EF����ʽ�뷴������������ʽ�����������ã�
2x2����2m+n��x+3��0��
x1+x2��![]() ��x1x2��
��x1x2��![]() ��
��
���F��![]() n��
n��![]() ����
����
��a��![]() ��
��![]() ����b��
����b��![]() ��n+
��n+![]() ����
����
![]() ��2��
��2��
��2���ʵ�E��EH��x�ύ�ڵ�H��
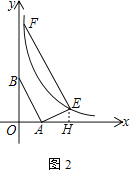
�ɣ�1��֪����ABO�ס�EHA��
��![]() ����EH��m����AH��2m��
����EH��m����AH��2m��
���E��2m+1��m������k��m��2m+1����2m2+m��
ֱ��AB����ʽ�е�kֵΪ��2��AB��EF����ֱ��EF����ʽ�е�kֵΪ��2��
��ֱ��EF�ı���ʽΪ��y����2x+b������E������벢���ã�b��5m+2��
��ֱ��EF�ı���ʽΪ��y����2x+5m+2��
����ʽ�뷴������������ʽ�����������ã�2x2����5m+2��x+3��0��
��Τ�ﶨ����ã�xF+xE��![]() ����xF��
����xF��![]() ��
��
���F��![]() m��4m+2����
m��4m+2����
��EF��![]() ��2AB��2��
��2AB��2��![]() ��
��
�����ã�3m2+4m��4��0��
��ã�m��![]() ��2����ȥ��ֵ����
��2����ȥ��ֵ����
k��m��2m+1����2m2+m��![]() ��
��

����Ŀ���������� ![]() ��7��ֵ�Ƕ��κ���
��7��ֵ�Ƕ��κ���![]() ͼ���ϵĵ�����Ӧ�����꣬����
ͼ���ϵĵ�����Ӧ�����꣬���� ![]()
x | �� |
|
|
|
|
|
|
| �� |
y | �� | 7 | m | 14 | k | 14 | m | 7 | �� |
���ݱ����ṩ����Ϣ��������4 ���жϣ�
�� ![]() ����
���� ![]() ���� ��
���� ��![]() ʱ��y ��ֵ�� k����
ʱ��y ��ֵ�� k���� ![]() �����ж���ȷ���� �� ��
�����ж���ȷ���� �� ��
A. �٢ڢ� B. �٢ڢ� C. �٢ۢ� D. �ڢۢ�