题目内容
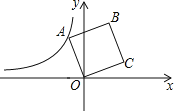
【题目】在Rt△ABC中,∠BAC=90°,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得△AFB,连接EF,下列结论:①△AED≌△AEF;②△ABC的面积等于四边形AFBD的面积;③BE+DC=DE;④BE2+DC2=DE2;⑤∠ADC=22.5°,其中正确的是( )

A. ①③④ B. ③④⑤ C. ①②④ D. ①②⑤
【答案】C
【解析】分析:①根据旋转的性质知∠CAD=∠BAF,AD=AF,因为∠BAC=90°,∠DAE=45°,所以∠CAD+∠BAE=45°,可得∠EAF=45°=∠DAE,由此即可证明△AEF≌△AED;
②根据旋转的性质,△ADC≌△ABF,进而得出△ABC的面积等于四边形AFBD的面积;
③根据①知道△ADE≌△AFE,得CD=BF,DE=EF;由此即可确定说法是否正确;
④据①BF=CD,EF=DE,∠FBE=90°,根据勾股定理判断.
⑤可以利用①②④正确,利用答案中没有更多正确答案,得出⑤错误.
详解:①根据旋转的性质知∠CAD=∠BAF,AD=AF.
∵∠BAC=90°,∠DAE=45°,∴∠CAD+∠BAE=45°,∴∠EAF=45°,∴△AEF≌△AED;
故①正确;
②∵根据旋转的性质,∴△ADC≌△ABF,∴△ABC的面积等于四边形AFBD的面积;
故此选项正确;
③根据①知道△ADE≌△AFE,得CD=BF,DE=EF,∴BE+DC=BE+BF>DE=EF,故③错误;
④∵AB=AC,△ADC旋转90°至△AFB,∴∠BAC=90°,∠ABC=∠ACB=45°,根据旋转的性质可得△ADC≌△ABF,∠ABF=∠ACD=45°,∴∠FBE=45°+45°=90°,∴BE2+BF2=EF2.
∵△ADC绕点A顺时针旋转90°后,得到△AFB,∴△AFB≌△ADC,∴BF=CD.
又∵EF=DE,∴BE2+CD2=DE2,故④正确.
⑤∵可以利用①②④正确,利用答案中没有更多正确答案,得出⑤错误.
故正确的有:①②④.
故选C.

【题目】某社区超市第一次用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 29 | 40 |
(1)该超市购进甲、乙两种商品各多少件?
(2)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(3)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元,求第二次乙商品是按原价打几折销售?