题目内容
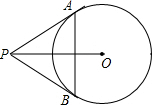
如图,⊙O的直径是10cm,PA,PB切⊙O于点A、B两点,若PO=13cm,则△PAB的周长为
cm.
分析:连接AO,BO,由PA与PB为圆O的切线,可得OA与AP垂直,OB与PB垂直,同时根据切线长定理得到AP=BP,PO为∠BPA的平分线,在直角三角形AOP中,由半径AO的长及OP的长,利用勾股定理求出AP的长,直角三角形APO的面积可以由两直角边乘以的一半来求出,也利用由斜边乘以斜边上的高的一半来求出,由AP=BP,PO为角平分线,根据三线合一得到OP垂直于AB,可得AC为斜边PO上的高,根据面积法求出AC的长,同时C为AB的中点,可得出AB=2AC,进而由AP+AB+PB可求出三角形APB的周长.
解答:解:连接AO,BO,
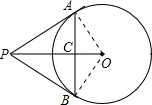
∵PA,PB为圆O的切线,
∴OA⊥AP,OB⊥BP,
又圆O的直径是10cm,
在Rt△APO中,OA=
×10=5cm,PO=13cm,
根据勾股定理得:AP=
=12cm,
根据切线长定理得到:AP=BP,PO平分∠APB,
∴OP⊥AB,垂足为C,
∴C为AB的中点,
又S
△APO=
AP•OA=
OP•AC,
∴AC=
=
cm,
∴AB=2AC=
cm,
则△APB的周长=AP+AB+BP=12+
+12=33
(cm).
点评:此题考查了切线的性质,切线长定理,等腰三角形的性质,勾股定理,以及垂径定理,遇到圆的切线问题,常常连接圆心与切点,构造直角三角形,利用直角三角形的有关知识解决问题.同时注意切线长定理的运用.
练习册系列答案
相关题目
 如图,⊙O的直径是10cm,PA,PB切⊙O于点A、B两点,若PO=13cm,则△PAB的周长为
如图,⊙O的直径是10cm,PA,PB切⊙O于点A、B两点,若PO=13cm,则△PAB的周长为 ∵PA,PB为圆O的切线,
∵PA,PB为圆O的切线, ∵PA,PB为圆O的切线,
∵PA,PB为圆O的切线,
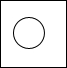 如图,圆的直径是正方形边长的一半,圆位于正方形的内部.现随意地将飞镖掷向正方形内,则镖击中圆面部分的概率是( )
如图,圆的直径是正方形边长的一半,圆位于正方形的内部.现随意地将飞镖掷向正方形内,则镖击中圆面部分的概率是( )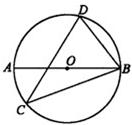 10、如图,⊙O的直径是AB,CD是⊙O的弦,若∠D=70°,则∠ABC等于
10、如图,⊙O的直径是AB,CD是⊙O的弦,若∠D=70°,则∠ABC等于 11、如图,圆的直径是10厘米,A、B、C、D分别为正方形各边的中点,则图中阴影部分的面积是
11、如图,圆的直径是10厘米,A、B、C、D分别为正方形各边的中点,则图中阴影部分的面积是 如图,⊙O的直径是10,弦AB=8,P为AB上的一动点,求OP的范围.
如图,⊙O的直径是10,弦AB=8,P为AB上的一动点,求OP的范围.