题目内容
 如图,⊙O的直径是10,弦AB=8,P为AB上的一动点,求OP的范围.
如图,⊙O的直径是10,弦AB=8,P为AB上的一动点,求OP的范围.分析:找到两个极值点,①点P与点A或点B重合时OP取得最大,此时OP=5,当OP⊥AB时,OP取得最小,从而求出OP的取值范围.
解答:解:①当点P与点A或点P重合时,OP=r=5;
②如图所示:

∵OP⊥AB,
∴AP=PB=
AB=4,
在Rt△OPB中,OP=
=3.
综上可得OP的取值范围为:3≤OP≤5.
②如图所示:

∵OP⊥AB,
∴AP=PB=
| 1 |
| 2 |
在Rt△OPB中,OP=
| OB2-BP2 |
综上可得OP的取值范围为:3≤OP≤5.
点评:本题考查了垂径定理的知识,平分弦的直径平分这条弦,并且平分弦所对的两条弧,需要同学们熟练掌握.

练习册系列答案
相关题目
 如图,圆的直径是正方形边长的一半,圆位于正方形的内部.现随意地将飞镖掷向正方形内,则镖击中圆面部分的概率是( )
如图,圆的直径是正方形边长的一半,圆位于正方形的内部.现随意地将飞镖掷向正方形内,则镖击中圆面部分的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
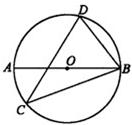 10、如图,⊙O的直径是AB,CD是⊙O的弦,若∠D=70°,则∠ABC等于
10、如图,⊙O的直径是AB,CD是⊙O的弦,若∠D=70°,则∠ABC等于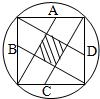 11、如图,圆的直径是10厘米,A、B、C、D分别为正方形各边的中点,则图中阴影部分的面积是
11、如图,圆的直径是10厘米,A、B、C、D分别为正方形各边的中点,则图中阴影部分的面积是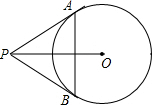 如图,⊙O的直径是10cm,PA,PB切⊙O于点A、B两点,若PO=13cm,则△PAB的周长为
如图,⊙O的直径是10cm,PA,PB切⊙O于点A、B两点,若PO=13cm,则△PAB的周长为