题目内容
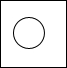 如图,圆的直径是正方形边长的一半,圆位于正方形的内部.现随意地将飞镖掷向正方形内,则镖击中圆面部分的概率是( )
如图,圆的直径是正方形边长的一半,圆位于正方形的内部.现随意地将飞镖掷向正方形内,则镖击中圆面部分的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
分析:根据题意,设圆的半径为1,可得正方形的面积与圆的面积,根据几何概率的求法,镖击中圆面部分的概率为圆与正方形的面积比,计算可得答案.
解答:解:设圆的半径为1,则正方形的边长为4,
有正方形的面积为16,圆的面积为π,
根据题意,镖击中圆面部分的概率即圆的面积与正方形的面积比,
故其概率为
;
故选D.
有正方形的面积为16,圆的面积为π,
根据题意,镖击中圆面部分的概率即圆的面积与正方形的面积比,
故其概率为
| π |
| 16 |
故选D.
点评:用到的知识点为:概率=相应的面积与总面积之比.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 如图,直径为1的圆与数轴有唯一的公共点P,点P表示的实数为-1,若该圆沿数轴正方向滚动一周后与数轴的公共点为P′,则点P′所表示的数是
如图,直径为1的圆与数轴有唯一的公共点P,点P表示的实数为-1,若该圆沿数轴正方向滚动一周后与数轴的公共点为P′,则点P′所表示的数是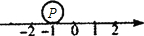 如图,直径为1的圆与数轴有唯一的公共点P,点P表示的实数为-1,若该圆沿数轴正方向滚动一周后与数轴的公共点为P′,则点P′所表示的数是________.
如图,直径为1的圆与数轴有唯一的公共点P,点P表示的实数为-1,若该圆沿数轴正方向滚动一周后与数轴的公共点为P′,则点P′所表示的数是________.