��Ŀ����
����Ŀ��ij���廧����һ��ʱ��ˮ����20��������ϣ���������������������˸��ټ�¼����������¼�����ݻ������µĺ���ͼ��������������y(ǧ��)������ʱ��x(��)֮��ĺ�����ϵ��ͼ(1)��ʾ�����۵���p(Ԫ/ǧ��)������ʱ��x(��)֮��ĺ�����ϵ��ͼ(2)��ʾ��(���۶�=���۵��ۡ�������)
(1)ֱ��д��y��x֮��ĺ�������ʽ��
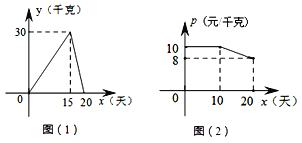
(2)�ֱ����10��͵�15������۶
(3)����������������24ǧ�˵�ʱ���Ϊ����������ڡ�����˴����۹����У�����������ڡ����ж�����?�ڴ��ڼ����۵������Ϊ����Ԫ?
���𰸡��⣺��1��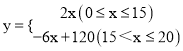 ��
��
��2������10��͵�15���ڵ�10��͵�20��֮�䣬
����10��x��20ʱ�������۵���p��Ԫ/ǧ�ˣ�������ʱ��x���죩֮��ĺ�������ʽΪp=mx+n��
���㣨10��10������20��8����z=mx+n��ͼ���ϣ�
��![]() ����ã�
����ã� 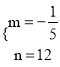 ��
��
��![]() ��
��
��x=10ʱ�� ![]() ��y=2��10=20�����۽��Ϊ��10��20=200��Ԫ����
��y=2��10=20�����۽��Ϊ��10��20=200��Ԫ����
��x=15ʱ�� ![]() ��y=2��15=30�����۽��Ϊ��9��30=270��Ԫ����
��y=2��15=30�����۽��Ϊ��9��30=270��Ԫ����
�ʵ�10��͵�15������۽��ֱ�Ϊ200Ԫ��270Ԫ��
��3������������������24ǧ�ˣ���y��24��
��0��x��15ʱ��y=2x��
�ⲻ��ʽ2x��24����x��12��
��15��x��20ʱ��y=��6x+120��
�ⲻ��ʽ��6x+120��24����x��16��
��12��x��16��
�ࡰ��������������У�16��12+1=5���죩��
��![]() ��10��x��20����
��10��x��20����![]() ��0����p��x�����������
��0����p��x�����������
����12��x��16ʱ��xȡ12ʱ��p�����ֵ����ʱ![]() =9.6��Ԫ/ǧ�ˣ���
=9.6��Ԫ/ǧ�ˣ���
�ʴ˴����۹����������������������5�죬�ڴ��ڼ����۵������Ϊ9.6Ԫ
�������������������1������������������ۣ���0��x��15����15��x��20�����ÿһ�����������������������Ľ���ʽ���ٽ���֪���������룬���ô���ϵ������⣺
����0��x��15ʱ������������y������ʱ��x�ĺ�������ʽΪy=k1x��
��ֱ��y=k1x���㣨15��30������15k1=30�����k1=2��
��y=2x��0��x��15����
����15��x��20ʱ������������y������ʱ��x�ĺ�������ʽΪy=k2x+b��
���㣨15��30������20��0����y=k2x+b��ͼ���ϣ�
��![]() ����ã�
����ã� ![]() ��
��
��y=��6x+120��15��x��20����
������������֪y��x֮��ĺ�����ϵʽΪ�� 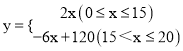 ��
��
��2�������۽��=�����۵������������������ڵ�10��͵�15���ڵ�10��͵�20��֮�䣬��10��x��20ʱ�������۵���p��Ԫ/ǧ�ˣ�������ʱ��x���죩֮��ĺ�����ϵʽΪp=mx+n���ɵ㣨10��10������20��8����p=mx+n��ͼ���ϣ����ô���ϵ�������p��x�ĺ�������ʽ���̶����10�����15������۽�
��3����������������24ǧ�ˣ���y��24���Ƚⲻ��ʽ2x��24����x��12���ٽⲻ��ʽ��6x+120��24����x��16������������������������5�죻Ȼ�����![]() ��10��x��20��������һ�κ��������ʣ���������ڴ��ڼ�����ʱ���۵����ֵ��
��10��x��20��������һ�κ��������ʣ���������ڴ��ڼ�����ʱ���۵����ֵ��