题目内容
【题目】已知，如图MN∥PQ，点A、B分别在MN、PQ上，∠ABP＝80°，射线BC平分∠ABP，且∠CAM＝25°，则∠ACB的度数为__________________.
【答案】15°或65°
【解析】
由于MN∥PQ，那么∠ADB=∠CBP，而∠ABP=80°，BC平分∠ABP，易求∠CBP，进而可知∠ADB，结合三角形外角性质分两种情况,当AC在直线MN的上方时和当AC在直线MN的下方时，可求∠ACB．
解：如图，
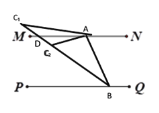
∵MN∥PQ，
∴∠ADB=∠CBP，
∵∠ABP=80°，BC平分∠ABP，
∴∠CBP=
∠ABP=40°，
∴∠ADB=40°，
当AC在直线MN的上方时，
∵∠ADB=∠CAM+∠C，∠CAM=25°，
∴∠C=∠ADB-∠CAM=40°-25°=15°．
当AC在直线MN的下方时，
∵∠ACB=∠ADB+∠CAM，∠CAM=25°，
∴∠ACB=40°+25°=65°．
故答案是15°或65°．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
