题目内容
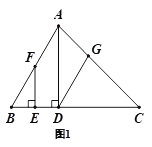
【题目】如图,直线AB∥FG,CE平分∠BCD,交FG于点E,过点D作DH⊥CE,垂足为H,若∠ABC=20°,则∠CEG-∠CDH=________度.
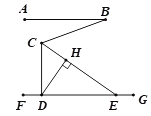
【答案】110°
【解析】
延长BC交FG于点M,根据AB∥FG,∠ABC=20°得∠CMD=20°,设∠CDH=x°,则∠DCH=∠BCE=90°- x°,则∠CEM==70°- x°,从而表示出∠CEG=110°+ x°,即可求出∠CEG-∠CDH的度数.
解:如图,延长BC交FG于点M,
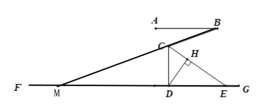
∵AB∥FG,∠ABC=20°,
∴∠CMD=20°,
设∠CDH=x°,
∵DH⊥CE,
∴∠DCH=90°- x°,
又∵CE平分∠BCD,
∴∠BCE=90°- x°,
∴∠CEM=∠BCE-∠CMD=90°- x°-20°=70°- x°,
∴∠CEG=180°-∠CEM=180°-(70°- x°)=110°+ x°,
∴∠CEG-∠CDH=110°+ x°- x°=110°,
故答案为: 110°.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
【题目】某学校的复印任务原来由甲复印社承包,其收费y(元)与复印页数x(页)的关系如下表:
x(页) | 100 | 200 | 400 | 1000 | … |
y(元) | 40 | 80 | 160 | 400 | … |
(1)根据表格信息写出y与x之间的关系式;
(2)现在乙复印社表示:若学校每月先付200元的承包费,则可按每页0.15元收费.乙复印社每月收费y(元)与复印页数x(页)之间的关系式为_______________;
(3)若学校每月复印页数在1200页左右,应选择哪个复印社?