题目内容
【题目】(1)问题发现.
如图1,![]() 和
和![]() 均为等边三角形,点
均为等边三角形,点![]() 、
、![]() 、
、![]() 均在同一直线上,连接
均在同一直线上,连接![]() .
.

①求证:![]() .
.
②求![]() 的度数.
的度数.
③线段![]() 、
、![]() 之间的数量关系为__________.
之间的数量关系为__________.
(2)拓展探究.
如图2,![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,点
,点![]() 、
、![]() 、
、![]() 在同一直线上,
在同一直线上,![]() 为
为![]() 中
中![]() 边上的高,连接
边上的高,连接![]() .
.

①请判断![]() 的度数为____________.
的度数为____________.
②线段![]() 、
、![]() 、
、![]() 之间的数量关系为________.(直接写出结论,不需证明)
之间的数量关系为________.(直接写出结论,不需证明)
【答案】(1)①详见解析;②60°;③![]() ;(2)①90°;②
;(2)①90°;②![]()
【解析】
(1)易证∠ACD=∠BCE,即可求证△ACD≌△BCE,根据全等三角形对应边相等可求得AD=BE,根据全等三角形对应角相等即可求得∠AEB的大小;
(2)易证△ACD≌△BCE,可得∠ADC=∠BEC,进而可以求得∠AEB=90°,即可求得DM=ME=CM,即可解题.
解:(1)①证明:∵![]() 和
和![]() 均为等边三角形,
均为等边三角形,
∴![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() .
.
②∵![]() 为等边三角形,
为等边三角形,
∴![]() .
.
∵点![]() 、
、![]() 、
、![]() 在同一直线上,
在同一直线上,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() .
.
③![]()
![]() ,
,
∴![]() .
.
故填:![]() ;
;
(2)①∵![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,
∴![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
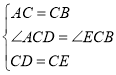 ,
,
∴![]() ,
,
∴![]() .
.
∵点![]() 、
、![]() 、
、![]() 在同一直线上,
在同一直线上,
∴![]() ,
,
∴![]() .
.
②∵![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() ,
,
∴![]() .
.
故填:①90°;②![]() .
.

练习册系列答案
相关题目






