题目内容
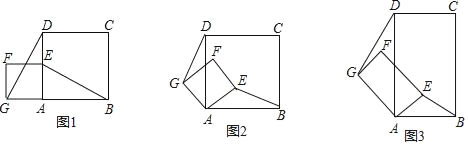
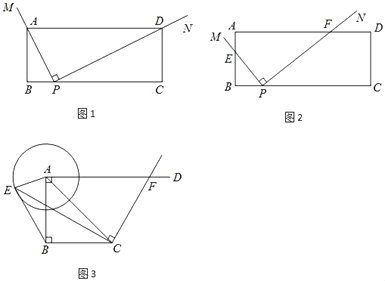
【题目】如图，AB⊥EF，DC⊥EF，垂足分别为B、C，且AB＝CD，BE＝CF．AF、DE相交于点O，AF、DC相交于点N，DE、AB相交于点M．
（1）请直接写出图中所有的等腰三角形；
（2）求证：△ABF≌△DCE．
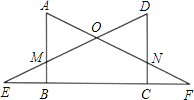
【答案】（1）△EOF，△AOM，△DON；（2）证明见解析
【解析】
（1）可以证明△ABF≌△DCE，根据全等三角形对应角相等可得∠A＝∠D，∠DEC＝∠AFB，所以△EOF是等腰三角形，再根据等角的余角相等可得∠A＝∠AMO，∠D＝∠DNO，从而得到△AOM与△DON也都是等腰三角形；
（2）由BE＝CF，可以证明EC＝BF，然后根据方法“边角边”即可证明△ABF与△DCE全等．
（1）解：△EOF，△AOM，△DON；
（2）证明：∵AB⊥EF于点B，DC⊥EF于点C，
∴∠ABC＝∠DCB＝90°，
∵CF＝BE，
∴CF+BC＝BE+BC，
即BF＝CE…
在△ABF和△DCE中，
，
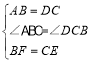∴△ABF≌△DCE，
练习册系列答案
相关题目
【题目】同时抛掷两枚硬币，按照正面出现的次数，可以分为“2个正面”、“1个正面”和“没有正面”这3种可能的结果，小红与小明两人共做了6组实验，每组实验都为同时抛掷两枚硬币10次，下表为实验记录的统计表：
结果 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 | 第六组 |
两个正面 | 3 | 3 | 5 | 1 | 4 | 2 |
一个正面 | 6 | 5 | 5 | 5 | 5 | 7 |
没有正面 | 1 | 2 | 0 | 4 | 1 | 1 |
由上表结果，计算得出现“2个正面”、“1个正面”和“没有正面”这3种结果的频率分别是___________________．当试验组数增加到很大时，请你对这三种结果的可能性的大小作出预测：______________．
